Matte E - Derivator och integraler
Volymberäkningar
Volymen av rotationskroppar – Rotation kring x-axeln
Formeln för hur vi räknar ut volymen av rotationskroppar som roterar kring x-axeln ser ut så här:
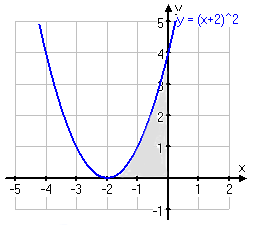Kurvan begränsar tillsammans med koordinataxlarna ett område. Beräkna volymen av den rotationskropp som alstras när området roterar kring x-axeln.
Det är bra att alltid rita upp kurvan på miniräknaren så man vet vilket område det handlar om. Här ser vi att den ena gränsen är x=0 eftersom y-axeln begränsade området. Den andra gränsen är där kurvan har sin minimipunkt eftersom den går ihop med x-axeln där. Då får vi ta fram den punkten med hjälp av derivatan.
Området det gäller ligger i intervallet
Minustecknet framför V sätter vi för att inte få en negativ volym då området ifråga är på den negativa sidan av x-axeln.
Svar: Volymen är 20,1v.e.
Rotation kring y-axeln
Då vi ska räkna ut rotationsvolymen av y-axeln så använder vi oss av samma formel som för rotationsvolymen för x-axeln, MEN, först måste vi göra om uttrycket så att x är en funktion av y. (I normala fall så är y en funktion av x.) Notera att integralen avslutas med dy.
Klotets volym
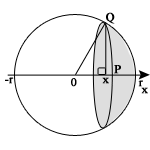Efter en liten krånglig härledning så kan man komma fram till att snittarean är:
Vi använder uttrycket:
då vi ska beräkna ett klotsegments volym.
Klotets volym är
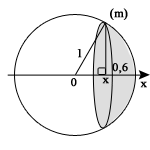Ett klotsegments har klotradien 1,0m och höjden 0,6m. Beräkna segmentets volym.
Då vi har ritat upp en bild av det hela är det mycket enklare att förstå. Vi ser att det har bildats en rätvinklig triangel, vars bas måste vara 0,4 då (radien 1)-(höjden 0,6) = 0,4. Punkten x är därför lika med 0,4.
Klotsegmentet kan ses som en rotationsvolym i intervallet
Svar: Volymen är 0,90m3.
16 februari 2011 @ 11:51
Hej!
Tack för att ni har skapat den här sidan, brukar hänvisa syskonen hit när de vill förstå mer (eller överhuvudtaget).
Har bara ett par saker att anmärka på. I exempel 1 säger er lösningsföljd att -V = 20,1 ve, vilket innebär att volymen ni räknat ut faktiskt är negativ, dvs V = -20,1 ve. Volymer ska ju inte vara negativa, och anledningen till det knasiga är följande:
Kalla den primitiva funktion för P(x). Ni vill integrera från -2 till 0, och då ges värdet av pi(P(0)-P(-2)), vilket ger pi*32/5. Det som hänt är att ni satt in gränserna i fel ordning: pi(P(-2)-P(0)), vilket då gör att ni måste multiplicera med -1 för att det ska stämma. Rätt vore alltså att antingen integrera från 0 till -2 och multiplicera med -1, eller från -2 till 0 och låta det vara.
MVH, Calle.
26 februari 2011 @ 15:32
Borde inte snittarean för klotet vara pi*(r^2-x^2). (Ovanför exempel 3). Ni har tagit radien gånger pi istället för radien i kvadrat gånger pi som man ska göra. Jag ser dock att ni har gjort rätt i exempel 3.
27 februari 2011 @ 12:34
Då vi ska räkna ut rotationsvolymen av x-axeln så använder vi oss av samma formel som för rotationsvolymen för x-axeln, MEN, först måste vi göra om uttrycket så att x är en funktion av y. (I normala fall så är y en funktion av x.) Notera att integralen avslutas med dy.
Ska stå y-axeln istället för x-axeln två ggr
Tack för en jättebra sida!
23 maj 2011 @ 19:55
“Då vi ska räkna ut rotationsvolymen av x-axeln så använder vi oss av samma formel som för rotationsvolymen för x-axeln”
ska det inte stå “Då vi ska räkna ut rotationsvolymen av ***y-axeln*** så använder vi oss av samma formel som för rotationsvolymen för x-axeln” ?
mvh anoar
PS: du/ni beskriver då bra simpelt och koncentrerat tack !
24 maj 2011 @ 8:03
@Anoar och Sofia: Tack för att ni båda uppmärksammat det lilla “tryckfelet”
Detta är nu korrigerat.
Kul att du tycker så Anoar! Då har jag lyckats med mitt mål med Matteguiden.
Mvh Elin E
21 mars 2012 @ 19:13
Vi har ett praktiskt problem: Om ett spår i marken skall fyllas med asfalt hur mycket går det åt? Spåret är 11 meter långt, 4 cm djupt och 6 mm brett. Vi blir inte överens om nollorna när vi räknar på detta. Går det åt 2,6 liter eller 26 liter?
21 mars 2012 @ 21:17
Vi gör om det till samma enhet så blir det lätte. Jag väljer att göra om det till dm för att 1 kubikdecimeter = 1 liter.
Spåret är 110 dm långt, 0.4 dm djupt och 0.06 dm brett. 110*0.4*0.06=2.64dm^3. Det blir ca 2.6 liter.