Matte 1 - Andelar
Procent, promille och ppm
Procent
Procent betyder hundradelar och skrivs %. Eftersom procent betyder hundradelar så måste 1% vara 1/100 (utläses en hundradel). Då man räknar med procent så utgår man ifrån att någonting är helt, det totala, alltså:
Skriv om följande procentsatser till decimalform
a) 40% b) 75%
a)
1% är en hundradel, vilket innebär att 40% måste vara 40 hundradelar. Dela 40 med 100 och du får 0,4.
b)
Samma sak här som i a-uppgiften. 75% lir 75 hundradelar. Om du delar 75 med 100 så får du 0,75. När du delar ett tal med 100 är det bara att flytta decimaltecknet två steg åt vänster.
Skriv om följande decimaltal till procentsatser
a) 0,68 b) 1,45 c) 0,05 d)
a)
0,68 är 68 hundradelar. 1 hundradel är en procent så då måste 68 hundradelar vara 68 procent.
b)
När decimaltalet är mer än 1 så är procentsatsen större än 100%.
c)
d)
Rektangeln nedanför är uppdelad i fem lika stora delar. Ange hur många procent utav rektangeln som är färgad.
![]()
Exemplet säger att rektangeln består av fem lika stora delar. Det innebär att en hel rektangel är 5/5 = 1 = 100 %. Om vi tittar på bilden så ser vi att två utav dessa fem delar är färgade. Vi kan då beräkna procentsatsen enligt följande:
Svar: 40% av rektangeln är färgad.
Beräkna delen då andelen är given
I följande underrubriker ska vi lära oss att beräkna delen, andelen respektive det hela. De olika namnen betyder:
delen=en del av det hela, anges i antal såsom kronor, styck. T.ex. 4 apelsiner av totalt 20 stycken.
andelen=anges i procent, decimaltal, bråktal. x% av det hela. T.ex. 60% av 20 apelsiner, 0,6, eller 3/5.
det hela=är helt enkelt det hela. T.ex. alla 20 apelsinerna.
I en korg ligger det 20 äpplen. Av dessa är röda äpplen. Hur många röda äpplen finns det i korgen?
Vi får reda på att andelen röda äpplen är . För att få reda på delen multiplicerar vi därför andelen med det hela:
Antalet röda äpplen är alltså 5 stycken.
Svar: Det ligger 5 röda äpplen i korgen.
Notera att också motsvarar 25%. Exemplet kunde alltså lika gärna sagt: “I en korg ligger det 20 äpplen. Av dessa är 25% röda äpplen“.
Beräkna andelen då delen är given
I en annan korg ligger det 18 gula och 12 röda paprikor. Beräkna andelen gula paprikor i korgen.
Vi vet redan delen gula paprikor, nämligen 18 stycken. Sammanlagt så liger det 12+18=30 paprikor i korgen. Nu när vi vet både delen och det hela så är det bara att räkna ut andelen:
Svar: De gula paprikorna utgör 60 procent av alla paprikorna i korgen.
Promille och ppm
Promille betyder tusendelar (‰) och ppm (parts per million) betyder, som ni kanske hör på namnet, miljondelar.
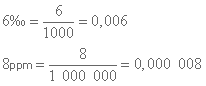
Som ni ser här ovan så ser promille tecknet nästan likadant ut som procenttecknet. Skillnaden är att man har lagt till en extra ring i slutet på tecknet. Promille betydde ju tusendel därför delas ett tal med tusen precis som procent, som betyder hundradel, delas med hundra.
Ppm betydde en miljondel, därför delas talet med en miljon och åttan placeras på platsen för miljondel.
Bestäm det hela då delen och andelen är givna
På Onoff var det dags för mellandagsrea och man beslöt då att sänka priset på alla datorer med 20%. En utav datorerna sänktes då med 1 200 kr.
a) Hur mycket kostade datorn från början?
b) Hur mycket kostade datorn efter sänkningen?
a) I uppgiften får vi veta att andelen är 20% och att delen således blir 1 200. Det hela, = datorns ordinariepris, blir alltså:
b) Datorn kostade 6 000 kr innan sänkningen. Dra nu bort 1 200 kr från detta:
6 000 – 1 200 = 4 800 kr
Svar: a) 6 000 kr b) 4 800 kr
Procentsatser större än 100%
Om priset för en vara har ökat med x antal kronor så kan vi beräkna hur många procent det nya priset är av det gamla priset. Det görs så här:
Priset på en antikvitet ökade från 800 kr till 1 200 kr. Med hur många procent ökade priset?
För att få fram hur många procent det nya priset är av det gamla priset delar vi det nya med det gamla:
Nu vet vi att det nya priset är 150% av det gamla priset. Eftersom det gamla priset är 100% så vet vi att det nya priset är 150%-100%=50% mer än det gamla. Priset har alltså ökat med 50%.
Svar: Priset ökade med 50%.
Procentenheter
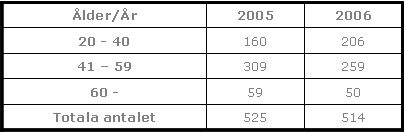
Här nedan ser vi en tabell över antalet rökare i olika åldrar på ett företag år 2005 och 2006.
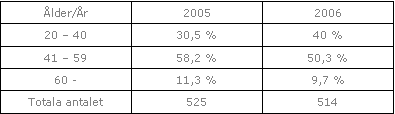
Där ser vi bland annat att andelen rökare i åldern 20 – 40 år har ökat. Där har de ökat från 30,5 % till 40 % vilket innebär en ökning på 40,0 % – 30,5 % = 9,5 procentenheter.
Procentenheter är alltså skillnaden mellan två procenttal. Vi skulle inte kunna säga att rökarna hade ökat med 9,5 procent för då skulle det bli helt fel. Säger vi procent istället så är det som om vi påstod att 40 vore lika med 9% av 30,5 och det är det ju inte. 9% av 30,5 är ca 2,7.
Hade det istället varit en tabell som visade antalet rökare i varje ålder (se nedan), och inte andelen, så hade man kunnat säga att rökarna i åldern 20-40 år hade ökat med 46 personer eller 46/160=0,2875 alltså 28,8%.