Matte 1 - Geometri
Trigonometri
Trigonometri
Trigonometri = triangelmätning. Inom trigonometrin spelar framförallt de rätvinkliga trianglarna en stor roll. Därför har man utvecklat några definitioner som gäller sambandet mellan en rätvinklig triangels sidor och dess vinklar. Innan vi bekantar oss med några nya formler så ska vi först klargöra några begrepp. I kapitlet om Pythagoras sats pratar vi om katetrar och hypotenusor.
Nu när vi ska studera sambandet kommer vi att specificera det lite genom att prata om motstående respektive närliggande katet.
Motstående katet är kateten mittemot den angivna vinkeln.
Närliggande katet är kateten närmast vinkeln.
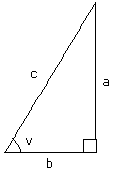
Om vi tittar på triangeln här intill så kan vi alltså konstatera att
a är motstående katet till vinkeln v
b är närliggande katet till vinkeln v
och precis som innan så är hypotenusan c i denna figur.
Sinus
Det samband mellan en rätvinkliga triangels sidor och vinklar som vi nämnde nyss kan ses om jämför tre likformiga trianglar, dvs. 3 olika stora rätvinkliga trianglar som har samma proportioner och lika stora vinklar.
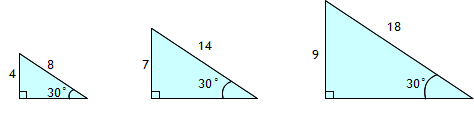
Vi ser att de är likformiga om vi jämför kvoten mellan motstående katet och hypotenusan:
Vi kan alltså konstatera: om vinkeln i en rätsidig triangel är 30° så är kvoten mellan motstående katet och hypotenusan alltid 0,5.
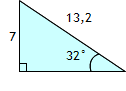
Om vinkeln istället hade varit t.ex. några grader större (32°) så skulle kvoten också bli lite större:
Vi kan se att för varje vinkel finns det också en specifik kvot. Kvoten vi har räknat fram nu kallas “sinus för vinkeln” och betecknas sin v.
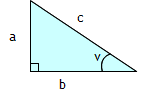
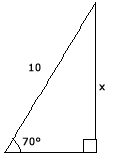Hur lång är sidan x i triangeln?
Om vi jämför vår triangel med den triangel som står tillsammans med reglerna så ser vi att det är sidan a vi ska räkna ut. vi ser också att vi vet vinkeln v och sidan c. Vi ska då använda formeln .
Skriv upp formlen och sätt in de värden du vet och lös sedan ekvationen. Sidan a är ju x i detta fall.
Svar: Sidan x är 9,4 cm lång.
Cosinus och tangens
Precis som vi tog fram sinus kan vi även få fram definitionerna på cosinus och tangens genom att bilda två andra kvoter. Dels kan vi bilda en mellan närliggande katet och hypotenusan, dels kan vi bilda en kvot mellan motstående och närliggande katet. Dessa två kvoter motsvarar cosinus respektive tangens.
Hur lång är sidan x?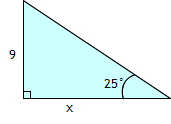
Vi börjar med att titta på det vi har fått veta. I detta fall vet vi att motstående katet = 9 och att vinkeln är 25°. Uppgiften är att beräkna den närliggande kateten. Den formel som innehåller alla tre delarna är formeln för tangens, dvs. tangens för vinkeln v.
Vi sätter in våra tal:
och vips så har vi en ekvation vi kan lösa!
Svar:
Hur lång är sidan x?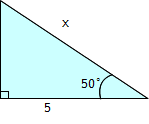
Återigen börjar vi med att titta på det vi har fått veta. Den här gången vet vi att närliggande katet = 5 och att vinkeln är 50°. Uppgiften är att beräkna hypotenusan. Den formel som innehåller alla tre delarna är formeln för cosinus, dvs. cosinus för vinkeln v.
Vi sätter in våra tal:
…och beräknar x:
Svar: Hypotenusan är 7,8
Sammanfattningsvis, kan vi konstatera att följande formler kan vara bra att använda sig av då man behöver räkna ut en viss sida i en triangel eller kanske någon utav dess vinklar. I regelrutan visas de tre reglerna för sinus, cosinus och tangens:
Detta gäller för en spetsig vinkel (v) i en rätvinklig triangel:
Beräkning av vinklar
Då vi ska bestämma en vinkel använder vi oss av uttrycket arcsin, arccos eller arctan. På miniräknaren står det ofta sin-1 etc istället. Då vi vet två stycken sidor i triangeln väljer vi den formel som passar bäst. Vet vi t.ex. längden på motstående och närliggande katet så är tangens det givna valet. Vi ställer upp ekvationen som vanligt och får då ett värde på tan v. Vinkeln v är i sin tur lika med arctan(värdet vi fick fram).
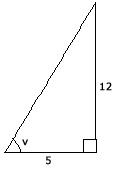Hur stor är vinkeln v?
Om vi åter igen jämför vår triangel med den som står vid reglerna så ser vi att den här gången vet vi sidan a och sidan b. Titta på reglerna för att se vilken formel som inkluderar de båda sidorna samt vinkeln v. Det är formeln vi ska använda oss av.
Sätt in de värden du vet i formeln och lös sedan ekvationen för att få fram vinkeln.
Vinkeln får ni fram genom att ta arctan2,4 (förmodligen tan-1 på era grafräknare).
Svar: Vinkeln v är 67,4°.