Matte 3 - Derivata
Ändringskvot och lutningar
Begreppet lutning – Räta linjer
Vi inleder detta kapitel med lite repetition kring begreppet lutning. Vi ritar upp en y- och en x-axel och sedan en rät linje som vi inte vet ekvationen för (Bild 1). Den generella ekvationen ser ju ut såhär: där k motsvarar lutningen. Här kommer vi nu bara att prata allmänt om räta linjer, alltså vi går inte in specifikt på vilka siffror den består av. Det tar vi senare i ett exempel längre ner.
Bild 1. En rät linje.
Hur var det nu vi skulle göra för att ta reda på lutningen för denna linje? Jo, för att kunna räkna ut lutningen så behövde vi ju få reda på hur mycket man har förflyttat sig i y-led då man tar ett steg i x-led. Det vi behöver göra är då alltså att ta ut två punkter på linjen för att kunna beräkna skillnaden mellan dem. Formeln för linjens lutning (eller riktningskoefficient) ser ut så här:
Formeln innebär att vi beräknar skillnaden i höjd mellan de två punkterna (Δy = y2-y1) och skillnaden i antalet steg på x-axeln (Δx = x2-x1) (Bild 3). Man pratar också om ändringskvoter, vilket formeln för lutningen ju är ett ypperligt exempel på. Vi beräknar nämligen kvoten mellan två förändringar dvs förändring i y-led och förändring i x-led.
Vi väljer dessa punkter i diagrammet:
Punkt 1 som består av x-koordinaten a och y-värdet motsvaras ju då av funktionens värde då man sätter in a i funktionen och räknar ut den.
Punkt 2 som utgörs av x-koordinaten b och y-värdet som fås då x-värdet sätts in i funktionen.
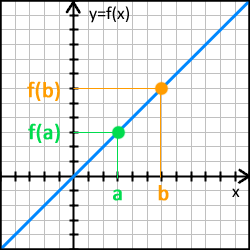
Bild 2. Vi tar ut två punkter på linjen.
Bild 3. Skillnaden mellan de båda punkternas y-värden motsvaras av Δy och skillnaden mellan x-värdena motsvaras av Δx.
Vi sätter in dessa punkter i ekvationen:
Om nu a hade motsvarat talet 3 och b motsvarat talet 6 samtidigt som de respektive y-värdena motsvarat 3 och 6 så hade vi fått följande uppställning:
…och kommit fram till att lutningen för denna linje är lika med 1.
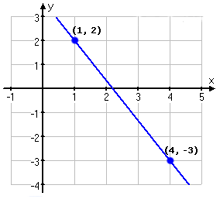Bestäm riktningskoefficienten (dvs lutningen) för den linje som går genom punkterna och
Vi låter den ena punkten motsvara och och den andra och
Notera att det inte spelar någon roll vilken punkt du börjar med:
Svar: Linjens lutning är
Om vi nu går över till det vi egentligen ska titta på i detta kapitel, nämligen olika kurvor och hur deras lutning förändras. Trots att en del av er kanske tyckte att ovanstående var ren repetition från Matte 2 så fanns det ändå en poäng att gå igenom lutningsbegreppet grundligt. Ha nu kvar det vi nyss gått igenom i bakhuvudet medan vi går över på att titta på olika kurvors lutning.
Kurvors lutning och Derivatans definition
Till skillnad från en rät linje så förändras hela tiden kurvornas lutning beroende på var någonstans längs x-axeln man befinner sig.
Bild 4. En rät linje har alltid samma lutning oavsett i vilken punkt man befinner sig.
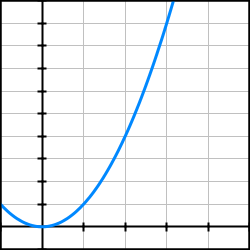
Bild 5. Hos en kurva så är lutningen olika i varje punkt.
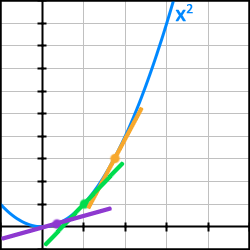
Bild 6. Hos en kurva så är lutningen olika i varje punkt, här är tangenter för respektive punkt utritad för att man ska se skillnaden i lutning.
En tangent är en linje som dras genom en kurvas punkt och som matchar lutningen på kurvan i just den punkten. Om vi märker ut några punkter och sedan ritar en tangent i vardera punkt så ser vi att tangenternas lutning skiljer sig från varandra. I detta fall ser vi att ju större värden på x, desto större blir lutningen på kurvan (Bild 6).
Låt oss säga att vi vill veta vad lutningen är i just punkten x (Bild 7a). Om vi ser till formeln för lutning så säger den ju att det krävs att man vet två punkter på linjen för att kunna beräkna lutningen. Vi tar därför och markerar en till punkt lite högre upp på axeln, men ändå relativt nära den punkten vi egentligen är intresserade av. Den andra punkten benämner vi x + h för att den ligger på avståndet h från x (Bild 7b).
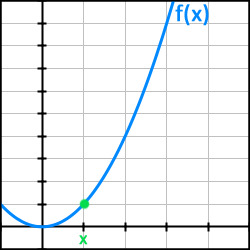
Bild 7a. Punkten x är markerad
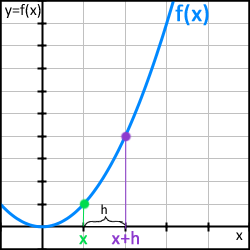
Bild 7b. Punkten x+h ligger på avståndet h från punkten x.
Dessa två punkter har ju även varsin y-koordinat. Om kurvans funktion är f(x) så blir respektive punkts y-koordinat f(x) samt f(x+h) (Bild 8a).
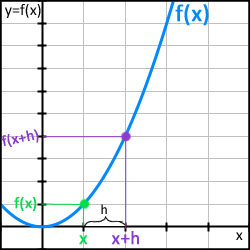
Bild 8a.
Bild 8b. Den oreanga linjen som är utritade mellan de båda punkterna är den s.k. sekanten. Δy och Δx utgör skillnaden i y-led respektive x-led.
Så om vi då ska räkna ut lutningen mellan dessa punkter – alltså vi beräknar inte lutningen i just punkten x, utan lutningen på den linje (”sekanten”) som ritas mellan våra två utmarkerade punkter (Bild 8b). En sekant korsar en kurva i två punkter, en tangent korsar en kurva endast en gång. Vi använder oss alltså åter igen av formeln för en linjes lutning där vi delar skillnaden i y-led med skillnaden i x-led.
Vi har nu fått fram ett uttryck för sekantens lutning, men denna lutning är ju inte densamma som lutningen i just punkten x. Däremot så kan vi konstatera att ju närmare punkten x vi går dvs ju mindre värde på h desto mer lik blir lutningen den lutning som råder i punkten x. Om h skulle vara 100 steg från x så skulle lutningen på sekanten skilja sig ganska mycket från lutningen i punkten x, men om h istället bara skulle vara 0,000 000 000 1 så skulle man istället få ett värde på sekantens lutning som skulle vara mycket nära det värde på lutningen i punkten x (Bild 9, Bild 10).
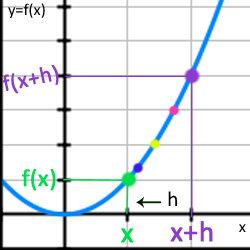
Bild 9. Om h skulle varit mindre än den är i den lila punkten. Här ses olika punkter som visar var x+h skulle hamnat om h hade haft ett mindre värde än vår lila punkt som vi utgått ifrån. Den blå punkten ligger mycket nära punkten x dvs h har i denna punkt ett mkt litet värde.
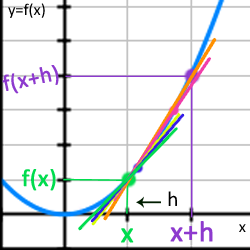
Bild 10. Här har vi ritat ut sekanter som dels skär kurvan i gröna punkten och sedan genom varsin punkt på kurvan. Den orangea sekanten är lutningen på linjen mellan den gröna och lila punkten, den rosa sekanten är lutningen på linjen mellan den gröna och rosa punkten osv. Vi ser att lutningen på den blå sekanten är väldigt lik den gröna linjens lutning som representerar lutningen i punkten x.
I detta sammanhang brukar man prata om lim som är en förkortning av det latinska ordet ”limes” (=gräns).
Vi kan konstatera att gränsvärdet för kurvan då är dvs alla x-värden som ligger tillräckligt nära punkten x ligger också väldigt nära y-värdet f(x).
Matematiskt skrivs detta som:
I och med detta kära vänner så har vi nu definierat det som inom matematiken kallas Derivatan! Funktionen som står här kan kallas ”Derivatan av funktionen f(x)” och skrivs även som ”f prim av x”:
Derivatans definition
På nästa sida tittar vi på hur vi använder detta uttryck i praktiken!