Matte 1 - Sannolikhetslära
Komplementhändelse
Här kommer vi att diskutera orden utfallsrum, händelse och komplementhändelse.
För att beskriva dessa utgår vi från ett slumpmässigt försök där vi, utan att se, ska plocka ett strumppar ur en låda. I lådan ligger det två par röda och två par svarta strumpor (totalt fyra par strumpor).
Begreppet händelse, syftar till det som faktiskt sker vid det slumpmässiga försöket, alltså utfallet eller flera utfall om vi gör fler försök i rad. Vi plockar en gång och får då upp ett rött strumppar, de läggs tillbaka och det slumpmässiga försöket upprepas, denna gång tar vi upp ett svart strumppar. Dessa två utfall är en händelse.
Begreppet komplementhändelse syftar till de utfall som inte ingår i en given händelse, alltså de utfall som faktiskt inte sker när man gör det slumpmässiga försöket.
Begreppet utfallsrum innebär mängden av alla möjliga utfall i ett slumpmässigt försök, dvs. i “rummet” ryms både händelse och komplementhändelse. Utfallsrummet kan ritas på olika sätt. Låt oss säga att vi har fyra strumpor i lådan, 2 röda och två svarta. Vi ska sedan plocka två strumpor, två gånger (strumporna läggs tillbaka efter varje plockning så det alltid är fyra stycken i lådan). Vi kan därefter rita upp resultatet i ett koordinatsystem där vi sätter ut de möjliga utfallen på respektive axel.
Utfallsrummet blir följande:
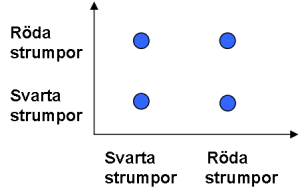
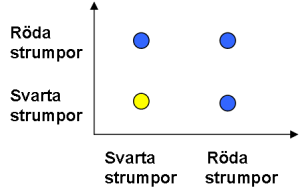
Prickarna utgör alla möjliga utfall, alltså hela utfallsrummet. Y- respektive x-axeln motsvarar varsin plockning (2 plockningar görs).
Låt säga att vi en gång får två röda strumpor och andra gången 1 röd och en svart strumpa. Om vi ritar in det i koordinatsystemet så ser det ut såhär:
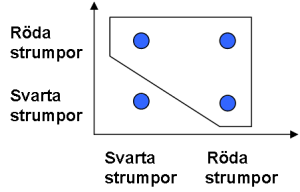
Förklaringen till markeringen är följande:
- (1) Utfallet “två röda strumpor” markeras i koordinatsystemet där röd på y-axeln möter röd på x-axeln.
- (2) Utfallet “1 röd och en svart strumpa” är den punkt där
- röd på y-axeln möter svart på x-axeln
- svart på y-axeln möter röd på x-axeln
(1)
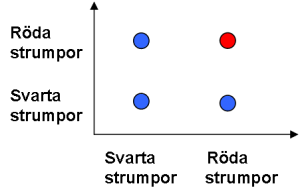
(2)
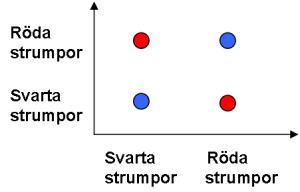
Komplementhändelsen i detta fall är den händelse som aldrig inträffade, dvs. en plockning där vi fick två svarta strumpor.
Likformig sannolikhetsfördelning
Om du känner att du har dålig koll på detta rekommenderar vi läsning på sidan Likformig sannolikhetsfördelning under Matte B innan exemplet gås igenom.
Du kastar två tärningar
a) hur stor är sannolikheten att siffersumman blir 6 eller mindre?
b) Vilka utfall utgör komplementhändelsen?
a)
Vi börjar med att rita upp utfallsrummet där alla möjligheter finns. Y-axeln motsvarar den ena tärningen, x-axeln motsvarar den andra tärningen. På varje axel skriver vi upp de möjliga tal som vi kan få då vi slår en tärning (1-6).

Utfallsrummet utgörs alltså av alla möjliga händelser/utfall som kan ske. Det vi nu ska göra är att markera en speciell händelse, nämligen händelsen där summan av de två tärningarna blir 6 eller mindre än 6. Vi ringar in de händelser där detta är fallet i vårt utfallsrum:

Som ni ser så uppfyller alla de inringade prickarna att deras summa är 6 eller mindre. Ta t.ex. punkten där utfallet är att båda tärningarna visar 1 när man slår dem (summan = 2), eller punkten där utfallet är att den ena tärningen visar 1 och den andra 5 (summan = 6).
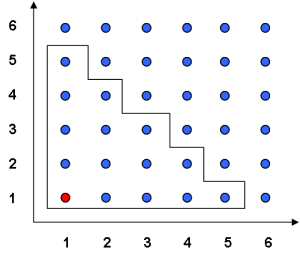

För att beräkna sannolikheten måste vi veta antalet möjliga utfall och hur många av dessa utfall som faktiskt inträffar. Vi ser i diagrammet att det finns 36 möjliga utfall och de som uppfyller våra krav på summan 6 eller mindre är 15 till antalet.
Sannolikheten att få summan 6 eller mindre är alltså:
b)
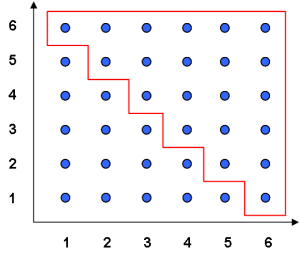
De utfall som utgör komplementhändelsen är de som inte uppfyller kravet summan 6 eller mindre, med andra ord, de utfall där summan har blivit större än 6. Om vi tittar i vårt diagram ser vi att det är 21 händelser som agerar komplementhändelser. Nämligen:
(6,1), (6,2), (6,3), (6,4), (6,5), (6,6), (5,2), (5,3), (5,4), (5,5), (5,6), (4,3), (4,4), (4,5), (4,6), (3,4), (3,5), (3,6), (2,5), (2,6) och (1,6).
Svar: a) Sannolikheten är . b) Händelserna (6,1), (6,2), (6,3), (6,4), (6,5), (6,6), (5,2), (5,3), (5,4), (5,5), (5,6), (4,3), (4,4), (4,5), (4,6), (3,4), (3,5), (3,6), (2,5), (2,6) och (1,6) är komplementhändelser.