Matte 1 - Sannolikhetslära
Försök i flera steg
Beroende och oberoende händelser
Om vi singlar slant två gånger i rad så vet vi att sannolikheten att få antingen klave eller krona är lika stor varje gång vi singlar slanten, alltså nästa slantsingling är inte beroende av utfallet på förra slantsinglingen.
Vi kan betrakta de två slantsinglingarna som oberoende händelser.
Om vi istället har en kulpåse med 5 blåa och 5 röda kulor och blir ombedda att plocka upp en kula åt gången så ser vi att sannolikheten förändras. Vid första plockningen är sannolikheten att få en blå eller en röd kula lika stor, det är ju lika många kulor i påsen. Låt säga att vi får upp en blå kula.
Vid andra plockningen däremot har förhållandena förändrats. I påsen ligger nu 5 röda kulor, men bara 4 blå. Det är nu något mer sannolikt att vi ska plocka en röd vid den andra plockningen.
Vi ser att den andra plockningen är beroende av utfallet i den första plockningen. Dessa plockningar är s.k. beroende händelser.
Produktregeln
Om vi åter tänker på slantsinglingen ovan. Händelsen att det blir krona vid ett försök är och händelsen att få klave . Hur stor är sannolikheten att man får krona i första försöket och klave i andra försöket?
För att kunna svara på detta kan vi ställa upp alla de möjliga utfallen, alltså de möjliga kombinationerna som kan inträffa:
krona krona
klave krona
krona klave
klave klave
De 4 olika utfallen är alla lika sannolika att inträffa dvs. alla utfallen har . Eftersom vår kombination “krona, klave” matchar en utav de möjliga utfallen är alltså
Detta värde är samma värde som vi får om vi multiplicerar sannolikheten för de båda händelserna med varandra:
Detta är ett exempel på produktregeln:
Produktregeln:
Sannolikheten för ett utfall i ett flerstegsförsök är lika med produkten av sannolikheterna för de olika händelserna som ses vid flerstegsförsöket.
Träddiagram
Ett vanligt sätt att beskriva ett slumpförsök är genom att använda ett träddiagram. Vi tar vårt exempel med när man singlar slant. De två utfallen är krona och klave.

I träddiagrammet nedan ser vi sannolikheten för varje utfall.

Om vi kastar myntet 2 gånger, ett s k dubbelkast, så är det ett exempel på ett försök i två steg. Kastar man fler gånger så kallas det för flerstegsförsök. Just flerstegsförsök beskrivs ofta med ett träddiagram.
Studera träddiagrammet här nedan.
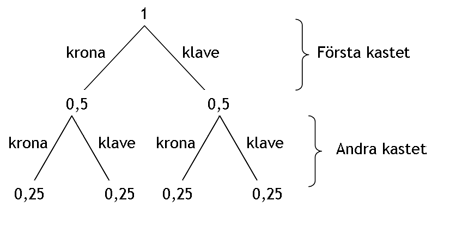
I detta fall så är det så att sannolikheten för om det blir krona eller klave i andra kastet är helt oberoende av vad som hände i första kastet. Vill vi beräkna sannolikheten för att man får klave två gånger i rad så skriver vi:
P(klave, klave) = 0,5 * 0,5 = 0,25
Sannolikheten för klave, krona blir således:
P(klave, krona) = 0,5 * 0,5 = 0,25
Ett annat exempel är om det nu skulle vara så att det andra försöket vore beroende av vad som hände i första försöket.
Örjan har 11 tröjor, varav 4 är röda och 7 är svarta. Örjan går fram till byrån där tröjorna ligger och plockar två tröjor på måfå.
Vad är sannolikheten att Örjan plockar
a) 2 röda tröjor b) 2 svarta tröjor c) 1 röd och 1 svart
Rita upp ett träddiagram och besvara uppgifterna.
Vi börjar med att rita upp ett träddiagram och fyller i de siffror vi vet.
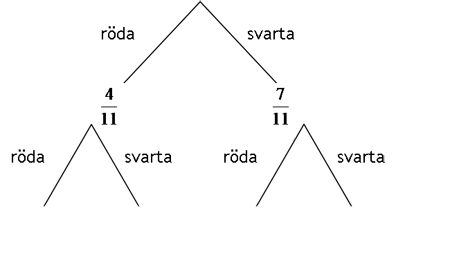
Vi vet sannolikheterna för första tröjan Örjan plockar. Där är sannolikheten för att det är en röd tröja 4/11 då det fanns 4 röda tröjor utav 11. På samma sätt är P för att den första tröjan är svart 7/11 då det fanns 7 svarta tröjor utav totalt 11.
Nu är det så att sannolikheten för de olika färgerna på den andra tröjan han plockar beror på vilken färg den första tröjan hade. Vi fortsätter att fylla i vårt träddiagram:
Om den första tröjan var röd så innebär det att det bara finns 3 röda tröjor kvar. Antalet svarta tröjor är fortfarande 7. Slutligen, det totala antalet tröjor är nu bara 10 eftersom han redan har plockat en.
Om den första tröjan istället var svart så innebär det att det nu finns 6 svarta kvar. Antalet röda är fortfarande 4. Likaså här är det totala antalet tröjor 10 stycken istället för 11.
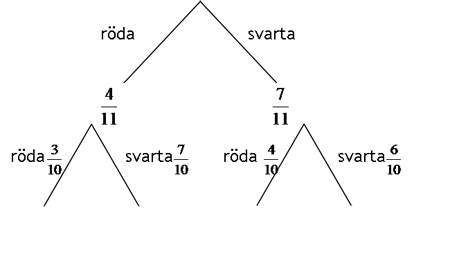
Då kan vi gå in på uppgifterna:
a) Här plockade Örjan 2 röda tröjor. Vi börjar då med att kolla sannolikheten för 1 röd tröja vid första ”plockningen”. Då var P(röd)=4/11. Efter det plockade han ännu en röd och denna gång var P(röd) istället 3/10.
Sannolikheten att han plockar 2 röda tröjor blir då enligt regeln ovan:
b) Då Örjan plockar 2 svarta tröjor så var sannolikheten för en svart tröja i första plockningen 7/11 och sannolikheten för en svart tröja även i andra plockningen 6/10. Alltså:
c) Då Örjan först plockar en röd och sedan en svart så är sannolikheten för en röd i första plockningen 4/11 och en svart i andra plockningen 7/10. Därmed får vi:
Det färdiga trädet ser således ut så här:
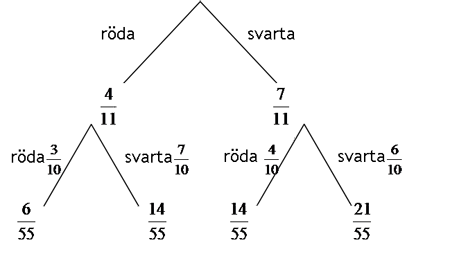
Svar: a) b) c)
6 maj 2016 @ 18:55
hello