Matte 1 - Statistik
Linje- och stolpdiagram
Linjediagram
Ett linjediagram är ett väldigt bra sätt att med en bild visa hur någonting förändras med tiden.
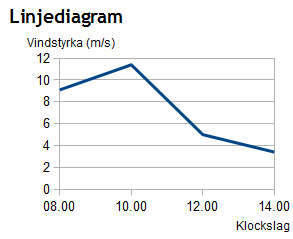
I vårt linjediagram här ovan ser vi hur vindhastigheten i en stad förändras mellan klockan 8 och 14. Vid 08.00 är den ca 9 m/s, vid 10-tiden har vindstyrkan ökat till dryga 11 m/s för att sedan vid 12.00 ha avtagit till 5 m/s osv.
Beräkna medelhastigheten för vinden mellan klockan 10 och 14.
Vi tittar på de värden vi har mellan klockan 10 och 14.
Klockan 10 är vindhastigheten 11 m/s
Klockan 12 är vindhastigheten 5 m/s
Klockan 10 är vindhastigheten 3,5 m/s
Medelvärdet beräknar vi genom att lägga ihop de tre värdena och delar sedan summan med 3.
Svar: Medelvindhastigheten var 6,5 m/s.
Stolpdiagram
Stolpdiagrammen liknar stapeldiagrammen till utseendet. Dessa är bra om man ska jämföra kvantitativa variablar som bara kan anta vissa värden t.ex. heltal.
Istället för att skriva kategorier under stolparna jämför vi olika numeriska värden och hur ofta de inträffar (frekvensen – y-axeln).
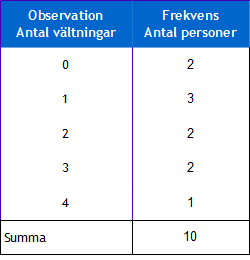
För över värdena i frekvenstabellen till ett stolpdiagram.
Som vi berättade på sidan om frekvenstabeller så motsvarar antalet vältningar olika observationsvärden. Varje sådant värde har en viss frekvens. För att visa detta ställer vi upp varje observationsvärde på x-axeln i rätt ordning alltså siffrorna räknas vilket gör att 0 vältningar står först, sen kommer 1 vältning osv.
När vi ritar upp y-axeln ser vi att vi behöver bara dra linjen så värdet 3 har plats, vi ritar upp till 5 för att få ett lite luftigare diagram. Därefter är det bara att fylla i de olika stolparna. Titta på hur många som välte 0 gånger, det var 2 stycken. Denna stolpe ritar vi ovanpå y-axeln fr det är där som 0 på x-axeln är.
Därefter tittar vi i tabellen hur många det var som välte 1 gång, det var 3 stycken som gjorde detta, alltså ritar vi stolpen så hög att den når upp i jämnhöjd med 3:an på y-axeln.
Upprepa samma sak för resterande observationsvärden och du får ett stolpdiagram likt det här nedanför:
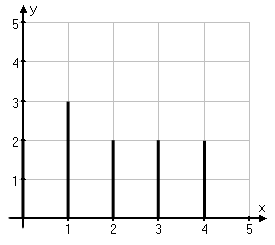
Histogram
Ett histogram är bra att använda då man har ett stort antal observationsvärden som är ganska spridda. Då kan det vara fördelaktigt att man delar in dem i klasser och sedan ritar upp dem i ett histogram.
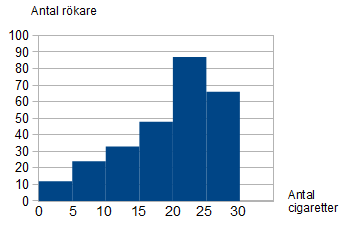
Vi har undersökt hur många cigaretter som rökare röker under en dag. Antalet cigaretter varierar mellan 1 och 30 stycken. Det vore väldigt knöligt att låta varje cigarettantal ha sin egen stolpe, vi skulle ju få 30 stolpar på x-axeln! Istället väljer vi att dela in antalet i följande kategorier.
- Rökare som röker 1-5 cigaretter om dagen
- Rökare som röker 6-10 cigaretter om dagen
- Rökare som röker 11-15 cigaretter om dagen
- Rökare som röker 16-20 cigaretter om dagen
- Rökare som röker 21-25 cigaretter om dagen
- Rökare som röker 26-30 cigaretter om dagen
Varje stapel i diagrammet motsvarar en grupp och höjden på respektive stapel är resultatet av att man har lagt ihop antalet rökare som ingår i varje grupp. Staplarna ligger precis kant i kant med varandra eftersom nästa grupp är en direkt fortsättning av den föregående grupp.
Ex. Det är 86 personer som röker 21-25 cigaretter om dagen. Vi kan inte säga exakt hur många som röker 23 cigaretter, men ofta är det inte så relevant om man röker någon cigarett mer eller mindre.