Matte 2 - Algebra och ickelinjära modeller
Andragradsekvationer
Definition
Andragradsekvationer kallas de ekvationer där variabeln är upphöjd till 2 t.ex. . Om variabeln hade varit upphöjd till 3 så hade det varit en tredjegradsekvation osv. Man använder alltså samma namngivning som för polynom av olika grader.
En ekvation har alltid lika många lösningar som dess grad anger. Med andra ord, en andragradsekvation har alltid 2 lösningar!
En andragradsekvation kan allmänt skrivas där a, b och c är konstanter och . Om a hade varit lika med noll så hade det ju inte funnits någon x2 och därmed hade vi inte haft någon andragradsekvation.
Det finns flera olika metoder för att lösa andragradsekvationer, vissa funkar alltid, andra funkar bara för specialfall.
Kvadratrotsmetoden
M h a kvadratrotsmetoden använder vi “kvadratroten ur” för att lösa ekvationer som enbart utgörs av variabeln upphöjt till två t.ex. .
Då vi tar kvadratroten ur ett tal så får vi inte glömma att skriva så här:
Som vi sa nyss, eftersom det är en andragradsekvation så har den två lösningar men vi ser bara en om vi inte sätter dit plus-minus-tecknet. Då vi kvadrerar ett negativt tal blir det ju positivt. Man kan dock aldrig ta roten ur ett negativt tal, sådana saknar lösning.
Denna andragradsekvation har de båda lösningarna och dvs. +7 och -7.
Nollproduktmetoden
Nollproduktmetoden går ut på att om en produkt är 0 så måste minst en utav faktorerna vara noll. Detta kan vi utnyttja i exemplet nedan:
Denna andragradsekvation kan vi faktorisera och därmed bryta ut x:
Vi ser nu att eftersom multiplikationen mellan x och (x+2) blir 0 så måste antingen x eller parentesen vara 0.
Första lösningen,
och andra lösningen fås genom
Nollproduktmetoden fungerar även för ekvationer med högre grad se exemplen nedan:
Lös ekvationen:
Den här ekvationen består av tre faktorer: x, (x+4) och (x+3) och är då en tredjegradare, vilket innebär att den har tre lösningar. Eftersom produkten är noll innebär det att någon utav dessa tre faktorer är lika med noll. Då sätter vi helt enkelt varje faktor lika med noll, vilket ger oss lösningarna:
Svar:
Lös ekvationen:
Här samlar vi först alla x på ena sidan och bryter sedan ut x-termen, alltså gör vi en faktoruppdelning/faktorisering.
Även här så måste någon av faktorerna vara lika med noll då produkten är noll.
Svar:
Kvadratkomplettering
Låt säga att vi har andragradsekvationen . Den kan inte lösas med någon av de metoderna som nämnts ovan utan här krävs det att vi använder kvadratkomplettering.
Kvadratkompletteringen går ut på att vi “kompletterar” vår ekvation med ett tal i kvadrat så att vänsterledet får utseendet som ett av de polynom vi associerar med kvadreringsreglerna. Vi tittar på ekvationen igen: – Vad är det för term som saknas för att vi ska kunna skriva om vänsterled m h a kvadreringsreglerna? Vi ser att både och är positiva alltså får vi anpassa oss till utseendet som fås via första kvadreringsregeln.
Jämförelse:
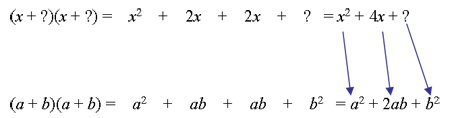
Vi ser att b2 ska motsvaras av 22, vilket vi sätter in i vår ekvation. Kom ihåg att det vi gör på ena sidan om likhetstecknet måste vi även göra på andra sidan likhetstecknet. Alltså sätter vi in även i högerled.
I och med detta kan vi skriva om vänsterled till enligt första kvadreringsregeln samtidigt som högerled bara beräknas:
Nästa steg i ekvationslösningen är att ta bort kvadreringen. Även detta måste göras i båda leden. För att ta bort kvadreringen tar vi roten ur då upphöjt till 2 och roten ur tar ut varandra. Vi tar även roten ur 16.
Om vi testar respektive x-värde genom att sätta in det i ursprungsekvationen så ser vi att det stämmer;
Lös ekvationen med kvadratkomplettering.
Vi börjar med att skriva om ekvationen till . Därefter behöver vi titta på vad vi ska komplettera med för kvadrat för att få ett uttryck som är rätt skrivet efter kvadreringsreglerna. I vänsterled ser vi som skulle motsvara:
enligt andra kvadreringsregeln. Vi inser att frågetecknet ska ersättas med siffran 1, alltså hälften av den siffra som står framför x-termen.
Då detta är en ekvation vi jobbar med så måste vi även kvadrera i högerled:
Enligt andra kvadreringsregeln motsvarar detta nu:
Nu tar vi bort kvadreringen genom att ta roten ur VL, detta måste även göras i HL:
Vi prövar lösningarna genom att sätta in dem i ekvationen var för sig:
Det stämmer! ![]()
Svar: x = 5 och x = -3
PQ-formeln
PQ-formeln är snabblösningen på det problem vi ställs inför när en andragradsekvation måste lösas med kvadratkomplettering. Det är en formel som är framtagen för att man snabbt och enkelt ska kunna få ut x-värdena utan att man själv behöver kvadratkomplettera.
PQ-formeln med lösning:
där p och q är konstanter. x² + px + q = 0 är den karakteristiska ekvationen för att lösningen på x ska bli möjlig.
Till exempel så måste x² alltså stå “ensamt”. Det får alltså inte vara 2x² + 2 + 4 = 0, för då fungerar inte pq formeln. Detta kan man dock enkelt lösa genom att dividera alla led med 2 i detta exempel, för att sedan kunna använda formeln.
Lös ekvationerna med hjälp av pq formeln:
a.)
b.)
c.)
a.)
b.)
c.)
Rotekvationer
Rotekvationer kallas sådana ekvationer som har det obekanta talet under rottecknet. Då man löser rotekvationer måste man kvadrera, vilket bidrar till att den nybildade ekvationen inte är lika med den förra ekvationen. Detta medför, då ekvationen är löst, att man har en falsk rot. Den falska roten upptäcks genom prövning, man testar om svaret är rätt genom att sätta in det i den ursprungliga ekvationen.
Lös ekvationen:
Börja med en förenkling:
Låt rottecknet stå själv på ena sidan och kvadrera sedan talen på båda sidorna. x-1 fås av att ‘roten ur’ är samma sak som ‘upphöjt i 0,5′ och när vi sedan kvadrerar så blir det en multiplikation av potenserna 0,5*2 = 1, alltså Notera också att vi använder pilenvid kvadreringen. Den betyder “medför att”.
Nu gör vi om ekvationen så vi kan lösa den med:
Nu ska vi avslöja den falska roten genom att testa de båda svaren i den ursprungliga ekvationen
Prövning ger:
HL = 5, VL = HL.
HL = 2, VL HL
(VL = Vänster led, HL = Höger led)
Svar:
Lösa rotekvationer med substitution
Substitution betyder i detta fall ”ersätta”, vilket är det perfekta ordet för det vi just nu ska göra. För att förklara denna metod behövs ett exempel.
Vi ska lösa ekvationen:
Om vi istället säger att där (vi ersätter ‘roten ur x’ med ‘u’) så får vi automatiskt att
Ursprungsekvationen ser då ut så här istället:
Om vi sedan flyttar över sexan till andra sidan av likhetstecknet så har vi hux flux en andragradsekvation som vi lätt kan lösa mha PQ-formlen! ![]()
ger oss eftersom
duger inte eftersom vi ställde villkoret att u skulle vara större än noll i början.
Svar:
Obs! Mycket viktigt att komma ihåg att svara med x och inte u, vilket många tenderar att glömma!
18 november 2015 @ 11:08
Hej!
Kom över denna sidan då jag letar bra exempel på rotekvationer. Såg dock exemplet med x^{2} 4x=12 här ovan och funderar varför det inte skulle gå att lösa den som alla andra andragradsekvationer genom att bara föra över 12 så det blir minus 12. Får ut 2 x som går att sätta in i den ursprungliga lösningen. x1=-6 och x2=2