Matte 2 - Algebra och ickelinjära modeller
Polynom
Definition av polynom
Ett polynom är ett matematiskt uttryck som består av positiva heltalspotenser av variabler och konstanter. Med andra ord, variablerna har utseendet där a är en konstant, x är variabeln och n är ett naturligt tal (positivt heltal). Variablerna och konstanterna kombineras genom addition, subtraktion eller multiplikation.
Man pratar om att polynom kan vara av olika grad. Denna grad baseras på det största värdet n antar. Dessutom får a inte vara lika med noll eftersom: .
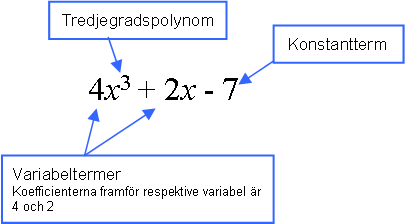
Exempel på uttryck som inte är polynom är:
Ett polynom ska består utav två termer t.ex. kallas för binom.
Räkna med polynom
Att addera och subtrahera polynom är inget avancerat. Det man ska komma ihåg är att man bara kan addera/subtrahera termer som har samma grad t.ex. och som blir om man adderar dem. Du kan inte addera t.ex. ett tredjegradspolynom med ett förstagradspolynom. Likaså räknar man med konstanterna för sig (en konstant är ett nolltegradspolynom).
När man multiplicerar polynom måste man dock ta hänsyn till en rad räkneregler. I detta exempel visar vi hur man multiplicerar 2 binom med varandra:
För dig som läsare finns det nu möjlighet att välja mellan att läsa en förklaring som berör varför man gör som man gör och en förklaring som enbart berättar hur man multiplicerar binom.
Förklaring för förståelse
Innan vi beräknar denna multiplikation så repeterar vi räknereglerna som styr då man multiplicerar ett tal med tal inuti en parentes:
Multiplikation prioriteras före addition. Alltså börjar vi med att multiplicera n med respektive tal som står inuti parentesen. Först n gånger x och sen n gånger -2. Det är viktigt att vi tar hänsyn till det tecken som står framför varje tal inuti parentesen. x:et är positivt vilket ger en positiv produkt, men 2:an är negativ så här får vi en negativ produkt.
Om vi nu ersätter n med ser det ut såhär:
I jämförelse med kan vi nu skriva såhär:
Alltså, när vi multiplicerar två binom (eller vid alla situationer med 2 parenteser med flera termer inuti sig) så multiplicerar vi varje term i den ena parentesen med varje term i den andra parentesen.
Förklaring enbart hur man gör
När du multiplicerar två binom (eller 2 parenteser med termer inuti sig) så multiplicerar du varje term i den ena parentesen med vardera term i den andra parentesen.
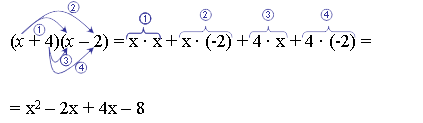
Börja med x i första parentesen och multiplicera den med x i andra parentesen vilket ger x2 och därefter med -2 vilket ger -2x. Därefter gör du samma sak med 4 i första parentesen: och .
Multiplicera följande polynom
a) b)
c)
a) Vi börjar med att multiplicera x:et i första polynomet med 2 och -x i det andra polynomet. Därefter upprepar vi samma sak med -5. Slutligen lägger vi ihop/subtraherar de termer som har samma grad, i detta fall har vi två termer som är förstagradare nämligen 2x och 5x.
Glöm inte att ta hänsyn till minus- och plustecken när du multiplicerar!
b)
Här har det ena polynomet tre termer, men vi gör på precis samma sätt ändå. Börja med att multiplicera i första parentesen med och -4 i andra parentesen. Upprepa därefter samma procedur med x respektive 2.
c)
Här spelar det ingen roll vilken multiplikation vi börjar med. Antingen börjar vi med att räkna ut eller .
Om vi börjar med måste vi sätta denna produkt inom parentes sen innan vi multiplicerar den med det andra binomet:
Svar: a) b)
c)
Kvadreringsregler
Dessa “regler” är snarare kom-ihåg-formler som underlättar för den som räknar att snabbt lista ut vad en multiplicering med två specifika binom blir.
Den första kvadreringsregeln beskriver vad resultatet blir om man multiplicerar ett binom med positiva termer med sig självt, alltså det kvadreras:
Om vi räknar ut det ser vi att vi får svaret
Om vi jämför denna uträkning med en generell uträkning med talen a och b så ser vi att man alltid får en produkt där första termen är binomets första term i kvadrat (a2), andra termen är resultatet av 2 stycken av första termen multiplicerat med andra termen i binomet (2ab). Slutligen får vi också en term som är resultatet av binomets sista term i kvadrat (b2).
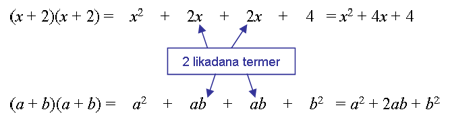
Den andra kvadreringsregeln beskriver samma sak som första, men här utgörs binomet av en positiv och en negativ term:
Jämför med
Skillnaden blir att produkten av de båda termerna (a och b) här blir negativ medan kvadraterna fortfarande är positiva.
När det gäller konjugatregeln så beskriver denna vad resultatet blir då man multiplicerat ett binom med två positiva termer med ett binom med samma termer fast där den ena termen är negativ:
Här tar den negativa och positiva termprodukterna (+2x och -2x) ut varandra och kvar får vi enbart första termen i kvadrat, respektive andra termen i kvadrat, som dessutom är negativ.
Första kvadreringsregeln:
Andra kvadreringsregeln:
Konjugatregeln:
Utveckla med hjälp av kvadreringsreglerna alternativt konjugatregeln
a) b)
c)
a) Vi utnyttjar första kvadreringsregeln:
b) Vi utnyttjar andra kvadreringsregeln:
c) Vi utnyttjar konjugatregeln:
Svar: a) b) c)
Faktorisera
Då min mattelärare ville att jag skulle använda faktoruppdelning skrek han alltid ”nötallergi” och då fattade jag direkt. Ordet nötallergi är nyckelordet för faktoruppdelning/faktorisering i min klass. Det han menar med nötallergi är att när man är nötallergiker så måste man alltid kolla på innehållsförteckningen innan man äter vissa saker. Faktoruppdelning eller faktorisering är precis samma sak, du måste kolla på innehållsförteckningen, alltså innehållet – faktorerna i ett tal som bygger upp produkten.
Faktorisering kan ibland vara smidigt att använda både vid ekvationslösning eller förenkling. Nedan presenteras två olika sätt att faktorisera polynom:
- Bryta ut största möjliga faktor
Man tittar på de faktorer som är gemensamma för alla de ingående talen och skriver sedan dessa utanför parentesen som kommer att innehålla de resterande faktorerna. T.ex:
Skriv ut faktorerna som bygger upp termerna i polynomet:
Vi ser att de gemensamma faktorerna för de båda termerna är ett x. Alltså skriver vi x som multipliceras med resterande termer som sätts inom en parentes.
Det rekommenderas att ni dubbelkollar ert svar genom att utföra multiplikationen mellan x och termerna inom parentesen så ni ser att ni får tillbaka ursprungstalet. - Använd kvadreringsreglerna och konjugatregeln “baklänges”
Om du t.ex. ser ett tal som är uppbyggt på samma sätt som kan du skriva det i formen . Talet kan skrivas om till .
Faktorisera
a) b)
a)
Nu ska vi dela upp respektive i sina respektive faktorer. består av 3·x·x och 5x består av 5·x. Vilka delar har de gemensamt? Jo, de har varsitt x. Den gemensamma faktorn sätter vi utanför parentesen som innehåller de tal som blir över.
b)
Återigen får vi ställa oss frågan: vilka faktorer består dessa produkter av? innehåller 2·x·x och 10 består av 2·5. Vilka faktorer har de gemensamt? Båda har en tvåa. Alltså blir det tvåan som står framför parentesen och resterande faktorer inuti parentesen:
Svar: a) b)
Det är mycket lätt att kolla om man gjort rätt i faktoruppdelningen. Om man utför multiplikationen i det svar man kommit fram till så ska man komma tillbaka till utgångsläget. Ex.
Vilket binom ska kvadreras för att ge ?
Om vi tittar på polynomets utseende så ser vi att den liknar det som bildas m h a den andra kvadreringsregeln:
och
Om vi nu ska ersätta med våra egna siffror så kan vi först och främst konstatera att det borde stå ett x som första term. Notera dock att vi i vårt fall har en konstant framför x:et, närmare bestämt en 9:a. Även denna siffra är enligt formeln kvadrerad, alltså borde det stå en 3:a framför x:et.
Nästa term (-18x) är resultatet av att man 2 gånger har multiplicerat första termen med andra termen och sedan lagt ihop dem. ska i det här fallet alltså ge 9x vilket måste innebära att den andra termen (b) motsvarar en 3:a.
Vi har nu kommit fram till att det kvadrerade binomet som ger upphov till är Detta tycks stämma även för konstanten 9 som är resultatet av att man har kvadrerat -3.
Svar: Det kvadrerade binomet är 3x-3.