Matte 3 - Derivata
Deriveringsregler
Derivatan av polynom
Nu ska vi äntligen lära oss det enkla sättet att räkna ut derivatan av en funktion!
Vi inleder med att titta på grafen till två enkla funktioner för att undersöka hur derivatans värde beror av dessa:
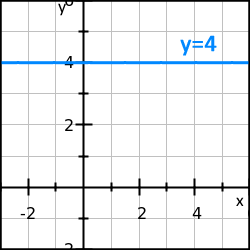
Bild 1. En konstant funktion.
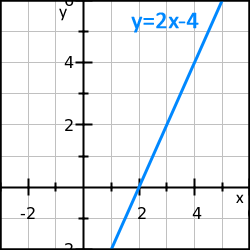
Bild 2. En funktion vars graf är en rät linje.
Som vi kan se i bild 1 så antar en konstant funktion alltid samma värde, dvs den förändras inte. Därmed är lutningen och också derivatan alltid noll oavsett x-värde.
Derivatan av en konstant
Då , där k är en konstant, så är
När det gäller funktioner vars graf är en rät linje, t.ex. som den i bild 2 så kan vi snabbt konstatera att en rät linje har samma lutning oavsett x-värde. Med andra ord kan vi konstatera att derivatan för sådana funktioner är densamma som linjens k-värde (riktningskoefficient).
Derivatan av en funktion
Då så är
Vi fortsätter vår undersökning med att försöka hitta ett mönster för derivatan av alla polynomfunktioner. Vi kikar lite närmare på funktionerna och .
Med hjälp av derivatans definition bestämmer vi respektive funktions derivata.
Derivatan för f(x)=x2
Derivatan för f(x)=x3
För att sammanfatta:
| Funktion | ||||
| Derivata |
Derivatan för , där n är ett positivt heltal, är .
Enkelt uttryckt, när du ska bestämma derivatan för en funktion så tar du talet som x:et är upphöjt till och sätter det framför x:et istället, därtill minskas det upphöjda talet med 1.
Om det därtill står en konstant framför x:et så innebär regeln nedan att du multiplicerar konstanten med det upphöjda talet som flyttas ned framför x:
Derivatan för , där n är ett positivt heltal och k en konstant, är .
Derivatan av ett polynom
Om man vill derivera funktionen så deriverar man termerna för sig. Det innebär att blir och blir 4. x är detsamma som , om vi deriverar detta polynom så multiplicerar vi fyran med ettan medan x:et istället blir upphöjt med noll. När man upphöjer ett tal till noll så blir det alltid 1.
Derivera följande funktioner:
a)
b)
c)
a)
Vi tar termerna var för sig, börja med som blir , därefter som blir 4 och slutligen 2 som blir 0.
b)
c)
Återigen, ta varje term för sig. I första termen multiplicerar vi 5 med 2:an framför x:et och minskar exponenten (det upphöjda talet) med 1. Nästa term sätter vi 2:an framför x:et och kvar blir . Slutligen har vi 3, som är en konstant och därmed försvinner helt vid derivering (se regeln ovan).
Svar: a) b) c)
Derivatan till , där a är ett reellt tal, är då .
Derivatan av exponentialfunktionen y=ekx
Detta stycke är under utveckling.
Derivatan till är , alltså är exponentialfunktionen lika med sin egen derivata.
Derivatan till är
Derivera följande funktioner
a)
b)
c)
d)
a)
b)
c)
d)
Svar: a) b) c) d).
Beräkna .
a)
b)
c)
a)
b)
c)
Svar: a) b) c).
I grafen ser du funktionen .
Genom att läsa av grafen, bestäm:
a)
b)
Slutligen, med hjälp av din grafräknare, bestäm
c) med en decimal.
a) , vi tittar var på y-axeln vi hamnar då vi markerar grafen i x-punkten 1,25. Detta blir värdet på funktionen.
b) , som regeln ovan säger så är ju derivatan av just . Med andra ord läser vi av grafen som vi gjorde i a-uppgiften och får då samma svar.
c) Knappa in på grafräknare och tryck ENTER.
Svar: a) b) c) .
Derivatan av exponentialfunktionen y=ax
Detta stycke är under utveckling.
Derivatan till är
Derivatan till är