Matte 1 - Funktioner
Exponentialfunktioner
En exponentiell förändring innebär att någonting ökar eller minskar i värdet med en viss procent för varje steg på x-axeln i ett diagram.
Nisse har gått och köpt en tavla för 10 000 på auktion. Man vet att konstnärens tavlor ökar i värde med tiden. Nisse är även intresserad av matematik och bestämmer sig för att räkna ut tavlans värde efter 10 år om
a) Nisse antar att tavlan ökar i värde med 1 000 kr per år?
b) Nisse antar att tavlan ökar i värde med 10% per år?
Vi börjar med att beteckna tiden med x år och tavlans värde med y kr.
a) I detta fall så ökar tavlans värde linjärt med tiden enligt följande samband:
där 10 000 är startvärdet, det den var värd nu när Nisse köpte den. 1000 kr är ökningen per år och x:et anger hur många år. 2 år ger till exempel 2 000 kr mer än 10 000 (1 000 · 2).
Om x= 10 så får tavlan värdet:
b) Om vi ska gå efter denna modell så blir tavlans värde efter
1 år
2 år
3 år
1,10 fås av att tavlans värde ska öka med 10%. (se Ändringsfaktor) När vi sedan ökar på med 2 respektive 3 år så multiplicerar vi varje års ökning med varandra (se Flera ändringar efter varandra), vilket resulterar i att man tar ökningen upphöjt till hur många gånger den görs.
10 år ger alltså
Om vi vill visa vad tavlar kostar efter x antal år skriver vi formeln:
vilket är en s.k. exponentialfunktion som beskriver ett förlopp där priset ändras med lika många procent hela tiden.
Om vi sätter in dessa värden samt de värdena för åren 4-9 så ser vi att de ligger på en jämnt böjd kurva i jämförelse med den linjära växten från a-uppgiften. Vi säger att värdet ökar exponentiellt med tiden.
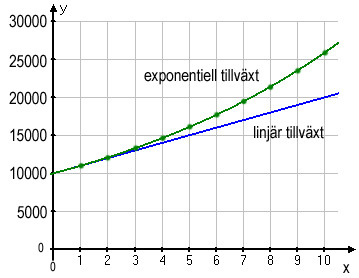
Vi ser att grafen blir brantare och brantare ju högre värden på x. Att exponentialfunktionen ” skenar iväg” ser man alltid, vilket beror på att varje gång en ökning görs får vi en större summa och det är med den nya större summan vi gör nästa ökningsberäkning. Ökningen blir alltså större och större i takt med att summan växer. 10% av 12 100 är ju mer än 10% av 10 000 osv.
Den karakteristiska exponentialfunktionen:
där C och a är konstanter och a är dessutom ändringsfaktorn.
Anton och Demir fick i uppgift att teckna ett uttryck för antalet bakterier i en bakteriekultur. Efter några minuter så kom de fram till att man kunde beräkna antalet bakterier med formeln , där t = antalet timmar efter att man började odla dem.
a) Beräkna och förklara med ord vad betyder.
b) Hur många bakterier fanns det efter 9,5 timmar?
a) N är antalet bakterier och N(t) betyder att antalet bakterier styrs av variabeln t. t var ju tiden i timmar efter det att man börjat odla dem. N(0) betyder att t=0 och då t=0 så har man ju bara hunnit börja med odlingen, allstå innebär N(0) att man räknar ut hur många bakterierna var från början. Ersätt t i formeln med 0:
b) Vi sätter att tiden t är 9,5, t=9,5. Sätt in detta i formeln och räkna ut värdet på N.
Svar: a) N(0) är antalet bakterier från början, vilket är 500 stycken.
b) Det är 538 bakterier efter 9,5 timmar.
20 november 2013 @ 17:49
hej vem kan hjälpa mig med de här
1) Bestäm ekvationen för en linje som går genom punkten (5, 2 ) och har riktningskoefficienten k= 2.
2) Bestäm ekvationen för den linje som går genom punkterna ( 1, 2 ) och ( 7 , 5 ).