Matte 1 - Funktioner
Funktionsbegreppet
Koordinatsystemet
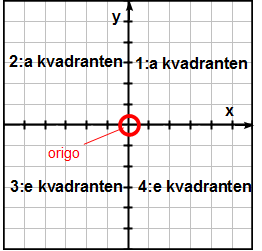Ett koordinatsystem utgörs av två tallinjer som korsar varandra i sina nollpunkter. Ett annat ord för dessa linjer är koordinataxlar. Man kallar den vertikala koordinataxeln för y-axeln och den horisontella för x-axeln så om vi har ett värde på x t.ex. 2 så vet vi att man menar punkten där 2:an på x-axeln ligger.
Punkten där koordinataxlarna korsar varandra kallas origo, och som sagt, det är här tallinjerna har sin nolla.
koordinatsystemet kan delas in i fyra rutor s.k. kvadranter – till dessa kan man hänvisa till när man t.ex. pratar om var någonstans en punkt ligger.
Ett koordinatsystem funkar lite som en karta, dvs man kan ange koordinater för att märka ut en viss plats (en punkts läge). Ta t.ex. punkt A i koordinatsystemet nedan:
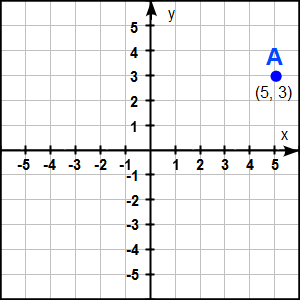
Då man anger koordinater så anger man var någonstans på x-axeln respektive y-axeln punkten ligger. Vi ser i bilden att A ligger på en punkt som är i jämnhöjd med x-axelns 5:a. Om vi tittar på hur punkten sedan ligger i förhållande till y-axeln så ser vi att den ligger på samma nivå som y-axelns 3:a.
Koordinater skrivs inom parentes där man först anger x-värdet följt av ett kommatecken och sedan y-värdet. Koordinaterna för punkt A ovan blir därför (5, 3).
Med hjälp av koordinater kan vi alltså exakt ange positionen för punkt p, vi vet var vi kan hitta den.
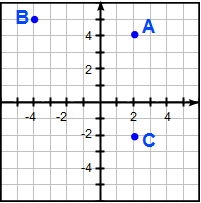Studera koordinatsystemet här till höger:
a) Ange koordinaterna för punkterna A, B och C i koordinatsystemet här intill
b) Beräkna avståndet mellan punkt A och C
c) Märk ut punkt D som har koordinaterna (-2, -4)
a) Ok, modellen för koordinatskrivning är att vi skriver först x-värdet och sen y-värdet (x, y). Vi börjar med punkt A och kikar på var den ligger i förhållande till x-axelns tal. Vi ser att den har x-värdet 2. Nu tittar vi på var A ligger i förhållande till y-axeln, vi ser att den ligger i höjd med y-värdet 4.
Koordinaterna för punkt A är således (2, 4).
Vi upprepar samma metod för punkt B och C och får koordinaterna:
B: (-4, 5)
C: (2, -2)
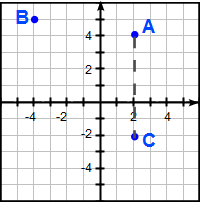b) Ett steg i koordinatsystemet kallas 1 längdenhet. Antingen räknar vi antalet rutor mellan de båda punkterna eller så beräknar vi skillnaden genom att ta A:s x-koordinat minus C:s x-koordinat.
Det är 6 rutor mellan de båda punkterna. alltså 6 längdenheter.
c) Punkt D ritar vi ut genom att först sätta pennan i på x-linjens värde (-2) och sedan går vi därifrån, ned mot y-linjens värde (-4). Då har vi hittat punkten med koordinaterna (-2, -4).
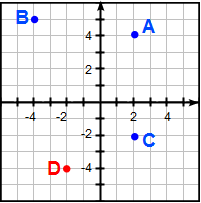
Svar: a) Koordinaterna för A:(2, 4), B: (-4, 5) och C: (2, -2) b) 6 längdenheter
c) se figur.
Funktioner
Under avsnittet Uttryck och formler pratade vi om att man kunde skriva ett uttryck för sträckan Demir hunnit köra beroende på antalet timmar han hade kört. Sambandet såg ut såhär:
Vi ser att om vi multiplicerar hastigheten 90 km/h med antalet timmar Demir kör så får vi fram sträckan i kilometer.
Det här sambandet kan illustreras på flera olika sätt t.ex:
EN VÄRDETABELL
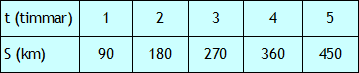
Värdetabellen visar sträckan (S) som en funktion av antalet timmar (t). I en värdetabell kan man läsa vad sträckan har för värde när t = 3 t.ex. Då t = 3 så är S = 270.
ETT FUNKTIONSUTTRYCK
Sambandet är tecknat som ett funktionsuttryck. Som vi nyss sa så är värdet på S beroende av värdet på t. Detta brukar man skriva som och man utläser det “S av t”.
Om vi vill visa vad S har för värde då t = 3 så ersätter vi helt enkelt t i formeln med 3:an:
OBS! När man pratar om funktioner i allmänhet så brukar man säga “f av x” dvs. funktionen av x då x är den vanligaste bokstaven man använder när man pratar om en variabel. Likaså, f är ganska naturligt att använda för man pratar ju om en funktion.. Ovanstående funktion skull i så fall se ut såhär: .
Det spelar egentligen ingen roll vilka bokstäver vi använder. vi kan skriva g(x), p(a) osv så länge man vet vilken bokstav som står för funktionens värde och vilken som är funktionens variabel.
Ibland betecknar man bara funktionen med en bokstav utan att skriva ut att x är variabeln t.ex.
Återigen, det spelar ingen roll vilka bokstäver/format du använder så länge du vet vad bokstäverna står för.
EN GRAF
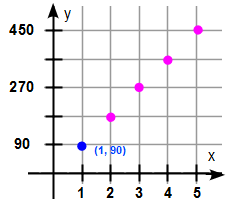I grafen är x-axeln graderad så vi kan utläsa antalet timmar och y-axeln så vi kan utläsa sträckans längd. I värdetabellen ovan kunde vi se de olika värdena för S beroende på t:s värde. Dessa värden fungerar som koordinater så vi kan märka ut dem i koordinatsystemet. Då t = 1 så var S = 90, vi markerar alltså punkten (1, 90). Upprepa med de andra punkterna.
Därefter drar vi en linje mellan dessa punkter och då har vi bildat en graf.
Man säger att grafen i bilden visar funktionen
En funktions värde utläses alltid på y-axeln och dess värde är beroende av variabelns värde som man utläser på x-axeln i ett koordinatsystem.
Funktionen f ges av . Beräkna
a) b) c) d)
a)
b)
c)
d)
Svar: a) 6 b) 6 c) 1 d) -6
Definitionsmängd och värdemängd
Definitionsmängden är de värden som variabeln (x) i en funktion kan anta.
Värdemängden är de värden som funktionen (y) kan anta. Grafen nedanför har definitionsmängden och värdemängden
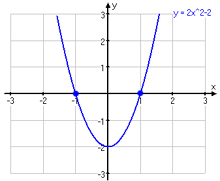
Definitionsmängd = alla tillåtna x-värden.
Värdemängd = de tillåtna värden som y kan anta.
Nollställen
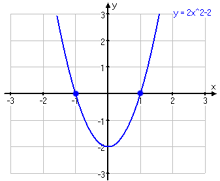
Nollställen kallas de ställen där funktionen f(x) antar värdet noll (y-axelns nolla), alltså där grafen passerar x-axeln. Funktionen i grafen här nedanför har nollställena x=-1 och x=1.
Bestäm nollstället till den linjära funktionen f.
a) b)
a) Nollstället är alltså det ställe där funktionen är lika med noll f(x)=0 eller y=0.
Alltså sätter vi funktionen är lika med noll:
b)
Svar: a) b)