Matte 1 - Funktioner
Linjära funktioner
Demir är återigen ute och kör med hastigheten 90 km/h. Han kör under tiden x timmar. Dagen innan hade han kört en sträcka på 100 km. Vi vill skriva en formel för hur lång sträcka han kör de båda dagarna.
Med hjälp av denna formel kan vi skapa en värdetabell och en graf för att titta på sambandet mellan K och x.
osv.
Som ni ser så motsvarar detta sambandet en rät linje i ett koordinatsystem och därför brukar man säga att sambandet är linjärt. Ni kan också se då x = 0 så är y inte lika med noll. det beror på att han startar ju andra dagen med att redan ha kört 100 km. 100 km blir startvärdet här.
Vi kan också skriva som och ser då att denna likhet är en ekvation.
Med andra ord: alla ekvationer som har utseendet motsvarar en rät linje när man ritar in den i ett koordinatsystem. m och k är konstanter, alltså tal som är desamma hela tiden. Demir håller konstant 90 km (k) och oavsett hur han kör dag 2 så har han avverkat 100 km (m) under gårdagen.
En linjär funktion kan alltid skrivas med formeln där k och m är konstanter.
En linjär funktion visas som en rät linje om man ritar upp dess graf.
ALGEBRAISK OCH GRAFISK LÖSNING
Om vi får frågan “Hur långt har Demir kört totalt om han kör 3 timmar andra dagen?” så kan vi lösa den på två sätt: antingen kan vi lösa det grafiskt eller algebraiskt.
Grafisk lösning innebär att vi helt enkelt tittar på grafen. Vi letar upp stället på grafen där x = 3 och läser av var på y-axeln vi befinner oss. Vi ser atty-värdet då x = 3 blir 370 km.
Algebraisk lösning innebär att vi räknar ut sträckan genom att sätta in 3:an i vår formel: .
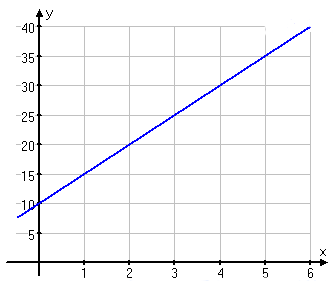Studera diagrammet här till höger och besvara frågorna.
a) Vilket y-värde svarar mot x=0?
b) Vilket y-värde svarar mot x=4?
c) Med hur mycket ökar y-värdet när x ökar från 0 till 4?
d) Hur mycket ökar y-värdet när x ökar med en enhet?
e) Skriv upp sambandet mellan y och x.
a) Följ den blå linjen tills du kommer till punkten där x=0. Läs sedan av y-värdet i samma punkt. I detta fall är y=10.
b) Gör likadant som i a-uppgiften, men här letar vi efter den punkt på linjen där x=4. Det ger oss ett y-värde på 30.
c) Kolla upp y-värdena för de båda punkterna x=0 och x=4, vilket vi reda gjort i uppgift a och b. För att veta hur mycket y har ökat så kollar vi differensen mellan de två värdena:
y har alltså ökat med 20.
d) Då x ökar med en enhet så innebär det helt steg på x-axeln. t.ex. från 3 till 4. Kolla upp y-värdet för båda de punkterna och beräkna därefter differensen på de båda värdena. x=3 ger y=25 och x=4 ger y=30.
.
y ökar alltså med 5 för varje enhet x ökar med.
e) Vi ser att den linjära funktionen utgår från 10 på y-axeln och i d-uppgiften räknade vi ut hur mycket y ökade för varje x-enhet. Det ger oss formeln .
Svar: a) y=10 b) y=30 c) y ökar med 20 d) y ökar med 5 för varje x-enhet. e) Sambandet mellan x och y lyder .
4 februari 2015 @ 13:09
va