Matte 3 - Trigonometri i trianglar
Rätvinkliga trianglar
Detta kapitel inleds med lite repetition från Trigonometrin i Matte 1.
Trigonometri
En viktig del inom trigonometrin är de definitioner som illustrerar sambandet mellan en rätvinklig triangels sidor och dess vinklar.
Bra att ha koll på: Pythagoras sats
Motstående katet är kateten mittemot den angivna vinkeln.
Närliggande katet är kateten närmast vinkeln.
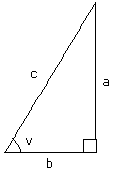
Om vi utgår från vinkeln v i den rätvinkliga triangeln här intill så är:
- a = motstående katet till vinkeln v
- b = närliggande katet till vinkeln v
- c = hypotenusan
och precis som innan så är hypotenusan c i denna figur.
Från vinkel till kvot
Beräkning av kvoten mellan två sidor då man vet vinkeln
Från kvot till vinkel
Beräkning av vinkeln då man vet kvoten mellan två sidor.
Notera att arctan, arcsin och arccos skrivs ofta som tan-1, sin-1, cos-1 på grafräknaren eller i vissa böcker.
Beroende på vilka sidor i den rätvinkliga triangeln som är angivna så får vi välja formel för vinkelberäkningen utefter det. Beräkna kvoten av dessa sidor och sätt sedan in det värdet i uttrycket arctan, arcsin eller arccos.
De olika värdena på tangens, sinus och cosinus är inbyggda i din grafritande räknare. Om man inte har tillgång till en sådan så finns det tabeller med motsvarande värden, t.ex. i en formelsamling.
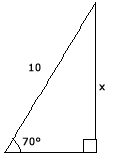Hur lång är sidan x i triangeln?
Om vi jämför vår triangel med den triangel som står tillsammans med reglerna så ser vi att det är sidan a vi ska räkna ut. vi ser också att vi vet vinkeln v och sidan c. Vi ska då använda formeln .
Skriv upp formlen och sätt in de värden du vet och lös sedan ekvationen. Sidan a är ju x i detta fall.
Svar: Sidan x är 9,4 cm lång.
Hur lång är sidan x?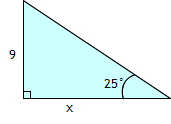
Vi börjar med att titta på det vi har fått veta. I detta fall vet vi att motstående katet = 9 och att vinkeln är 25°. Uppgiften är att beräkna den närliggande kateten. Den formel som innehåller alla tre delarna är formeln för tangens, dvs. tangens för vinkeln v.
Vi sätter in våra tal:
och vips så har vi en ekvation vi kan lösa!
Svar:
Hur lång är sidan x?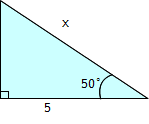
Återigen börjar vi med att titta på det vi har fått veta. Den här gången vet vi att närliggande katet = 5 och att vinkeln är 50°. Uppgiften är att beräkna hypotenusan. Den formel som innehåller alla tre delarna är formeln för cosinus, dvs. cosinus för vinkeln v.
Vi sätter in våra tal:
…och beräknar x:
Svar: Hypotenusan är 7,8
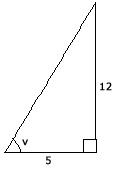Hur stor är vinkeln v?
Om vi åter igen jämför vår triangel med den som står vid reglerna så ser vi att den här gången vet vi sidan a och sidan b. Titta på reglerna för att se vilken formel som inkluderar de båda sidorna samt vinkeln v. Det är formeln vi ska använda oss av.
Sätt in de värden du vet i formeln och lös sedan ekvationen för att få fram vinkeln.
Vinkeln får ni fram genom att ta arctan2,4 (förmodligen tan-1 på era grafräknare).
Svar: Vinkeln v är 67,4°.