Matte A - Geometri
Skala och likformighet
Förminska och förstora
Figuren här nedan till vänster är i naturlig storlek medan den högra figuren bara är hälften så stor. Figuren till höger är en avbildning av figuren till vänster i skalan 1:2, som utläses ”ett till två”. Det betyder att 1 cm i den högra figuren motsvarar 2 cm i den vänstra/verkligheten.
Det vi såg exempel på här ovanför var en förminskning utav något. Här nedan ser vi istället en förstoring. Den högra bilden är fem gånger så stor som den vänstra bilden vilket innebär att varje centimeter i den vänstra figuren motsvara var femte centimeter i den högra. Skalan är alltså 5:1.
Dessa exempel bygger på att figurerna är likformiga, vilket betyder att kvoten mellan motsvarande avstånd på båda bilderna är likadan oavsett var någonstans i bilden det är. Kvoten är alltså skalan mellan figurerna.
I praktiken menar vi alltså:
Om vi har två bestämda avstånd i plutobilden t.ex. avstånd mellan plutos nos och svans respektive avståndet mellan framtass och baktass. Om plutobilderna är likformiga så har samma värde som .
Om det är svårt att komma ihåg hur man skriver skalan eller hur man tolkar skala kan ni tänka er att ni byter ut kolonet mellan siffrorna mot ett divisionstecken. I exemplen ovan så blir det i så fall 1/2 = 0,5 och 5/1 = 5. Detta innebär att den lilla Pluto är hälften så liten och den stora Musse 5 gånger så stor. Tänk bara på vilken bild det är man utgår ifrån!
Julia var ute och orienterade i skogen. Hon skulle till kontroll fem enligt kartan var det 2 km till den från det ställe där Julia stod. Hur långt var detta på karta om den var rita i skala 1:10 000? Svara i cm.
Börja först med att tolka skalan 1:10 000. Den skalan innebär att alla avstånd i verkligheten är 10 000 gånger större än motsvarande avstånd på kartan. Antag att avståndet på kartan är x cm. Alltså är
Gör om kilometer till centimeter:
2 km = 200 000 cm.
Sträckan mellan Julia och kontrollen är på kartan:
Svar: Sträckan är 20 cm på kartan.
Beräkna längder i likformiga figurer
Två figurer är likformiga om kvoten mellan motsvarande avstånd överallt är densamma. Kvoten är skalan mellan figurerna.
(Detta exempel är hämtat ur Gleerups Delta matematik kurs A och B.)
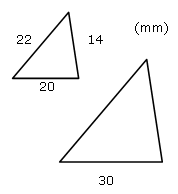
De två trianglarna till höger är likformiga. Beräkna längderna av de okända sidorna i den större triangeln.
Enligt regeln ovan så får vi fram skala mellan de båda figurerna genom att dividera de kända vågräta sidorna.
Förhållandet mellan den lilla och stora triangeln är 1:1,5, alltså den stora är 1,5 gånger så stor som den lilla.
Vi kan då beräkna de okända sidorna hos den stora triangeln genom att multiplicera 1,5 med den lilla triangelns sidor:
Svar: De två okända sidorna är 33 cm och 21 cm.
Areaskala
Areaskalan fungerar nästan likadant som vanlig skala. Det finns dock en liten skillnad. Arean betecknas ju i kvadrat 2 meter, cm osv. Alltså är areaskalan längdskalan i kvadrat.
Längdskalan: 0,2
Areaskalan: (0,2)2=0,04
Parallelltransversal
En parallelltransversal delar en triangel så att den får en topptriangel inuti den stora triangeln. Det råder likformighet mellan dessa två trianglar.
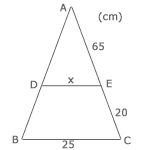Beräkna längden av sidan DE i triangeln ABC.
Linjen DE är en parallelltransversal och då vet vi att det råder likformighet mellan topptriangeln och triangeln ABC. Basen för topptriangeln benämns som x. Om vi delar topptriangelns högra sida med ABC-triangelns högra sida så får vi en kvot som ska vara densamma överallt. Ifall vi delar topptriangelns vänster sidan med ABC-triangelns vänstersida så ska den också ha samma kvot. Det gäller även för trianglarnas bas. x/25 ska alltså också ha samma kvot. Därmed kan vi ställa upp sambandet:
Eftersom både divisionen x/25 och divisionen 65/(65+20) har samma kvot så kan man sätta dem lika med varandra. (65+20) är ABC-triangelns högra sida där jag lägger ihop topptrinageln plus resterande från ABC-triangeln.
för att få fram längden på sidan DE så är det bara att lösa ut x ur ekvationen:
Svar: Sidan DE är 19 cm lång.
20 augusti 2010 @ 13:52
1km = 100 000cm (hundratusen)
20 augusti 2010 @ 14:27
Hej Daniel. Bra noterat. Jag har ändrat, så nu står det rätt på sidan.
18 oktober 2010 @ 11:24
Det står fortfarande 10 000x cm = 2km
18 oktober 2010 @ 20:48
Hej Simon.
Jag tror du har fel där. Det står rätt på sidan.
10 000x cm = 2km då x=20.
9 december 2010 @ 11:48
Hej! Hur gör jag om jag som här i ex. 3 istället ska räkna ut längden på BC med hjälp utav att jag vet att längden på DE är 19.
Tack på förhand!
20 oktober 2011 @ 14:46
Fel skala i svaret i exempel 2.
20 oktober 2011 @ 14:47
Enhet menar jag, förlåt.
20 oktober 2011 @ 15:17
Och är det inte så att AE i exempel 3 måste vara 64,6 cm om x=19?
8 december 2011 @ 17:40
Tack så jätte mycket
D
3 december 2014 @ 22:01
kan du hjälpa mig ska rita en pil på skala A) 5:1 och B) 1:3 vad ska jag göra fattar inte!! snälla hjälp
7 december 2014 @ 10:30
Skala 5:1 betyder att du ska rita den pil som du har fem gånger större.
(Om den ursprungliga pilen är 3cm blir den 15 cm lång)
Skala 1:3 betyder att du ska förminska den pilen 3 gånger.
(Om den ursprungliga pilen är 3cm blir den 1 cm lång)