Matte D - Integraler
Definition av integraler
Integraldefinition
En integral är arean av området ovanför x-axeln minus arean av området som är under x-axeln. Områdena begränsas av en funktion i intervallet.
Integralen betecknas så här:
utläses “integralen av f, från a till b”.
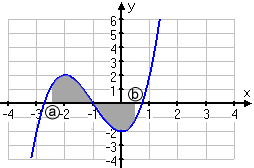
Det betyder att en funktion f(x) skrivs som primitiv funktion där x är variabeln (dx) och att den antar värden från a till b. a är den undre gränsen och b är den övre gränsen.
Svaret på en integral blir en siffra och siffran står för antalet ”areaenheter”. 1 a.e. motsvarar 1 ruta i ett koordinatsystem.
Integralen av styckvis linjära funktioner
Här är en alternativ metod till att beräkna en integral, men den funkar bara om funktionerna i fråga är linjära i det aktuella området, alltså de består av en rät linje i det området. Se här nedan:
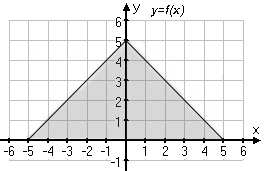
Det aktuella området för den här integralen vi ska beräkna bildar en triangel, och vi ser tydligt var någonstans de båda linjerna skär y-axeln respektive x-axeln. Avståndet mellan de båda punkterna på x-axeln är differensen mellan 5 och -5 vilket blir 10. Basen på triangeln är alltså lika med 10. Höjden på triangeln är det värdet där de båda linjerna skär y-axeln, alltså 5. Vi vet nu båda basen och höjden på triangeln och kan nu lätt räkna ut arean för den, viket också är svaret på integralens värde. Man ska inte krångla till saker i onödan. ![]()
Beräkna integralen
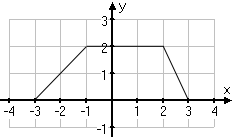
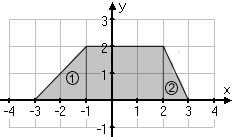
Här kan vi dela in bilden i 2 trianglar respektive en rektangel.
Triangel 1 har basen 2 då det är 2 steg mellan -3 och -1 på x-axeln, höjden är också 2 då linjen börjar vid 0 och slutar på 2 på y-axeln.
Triangel 2 har basen 1, då det är ett steg mellan 2 och 3 på x-axeln. Höjden är 2 då även denna linje börjar vid 0 och slutar vid 2 på y-axeln.
Rektangeln har basen 3 då det är 3 steg mellan -1 och 2 på x-axeln, och höjden är 2 då det är 2 steg mellan 0 och 2 på y-axeln.
Vi räknar ut respektive area och lägger sedan ihop dem alla 3 och därmed får vi svaret på vår integral.
Triangel 1:
a.e.
Triangel 2:
a.e.
Rektangel:
a.e.
Alltså:
a.e.
19 maj 2010 @ 22:01
På föregående sida skrev ni att integraler är derivatan baklänges… och det stämmer ju inte! det är ju primitiva funktionen som är som derivata fast tvärtom. akta så ni inte förvirrar oss :S
19 maj 2010 @ 22:45
Det stämmer. Jag tar bort det som är fel.
13 maj 2012 @ 1:43
awesome