Matte D - Trigonometriska funktioner
Trigonometriska funktioner 1
Eftersom detta avsnitt är väldigt långt så har jag delat upp det i två delar för att minska laddningstiden av sidan.
Kurvorna y = sin x och y = cos x
Här nedan har jag gjort en tabell över olika värden som sin x respektive cos x antar för de olika vinklarna på x:
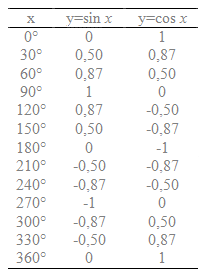
Om vi nu ritar upp detta i ett koordinatsystem så kan vi få en hyfsad graf till y=sin x och y=cos x. Du kan även rita upp den i din miniräknare, men för att få rätt bild så måste radianer vara markerat under MODE.

Vi ser ganska tydligt att kurvorna är jämna och symmetriska, detta beror på att de är så kallade periodiska. Då en kurva är periodisk så innebär det att kurvan upprepas varje 360°, alltså kurvstycket 0° till 360° upprepas regelbundet. Den har även den egenskapen att den kan dras ut åt både höger och vänster. Perioden kollar vi upp genom att kika på avståndet mellan två toppar alternativt två dalar (se vid gradpunkterna -90° och 270° samt 90° och 450°).

I bilden här nedan så har jag ritat de båda graferna i intervallet

Om vi jämför dessa två kurvor så ser vi att om vi flyttar sinuskurvan 90° åt vänster så får vi cosinuskurvan. Vi ska alltså lära oss hur en sådan och liknande förflyttningar påverkar kurvans ekvation.
Kurvorna y = Asin (x + v) och y = Acos (x + v)
Nu när vi vet hur kurvan y=sin x ser ut i grunden så nöjer vi os med att rita upp den endast med hjälp av vinklarna 0°, 90°, 180, 270° och 360°. Dessa fyra vinklar ger oss värdena 0, 1, 0, -1 och 0. (Detta kommer vi fram till genom att helt enkelt knappa in sin 90° osv på vår klipska miniräknare, MEN se till att grader är markerade i MODE. Vinklar som dessa kan även kollas upp i enhetscirkeln, det blir dock svårare att använda den då vi kommer in på andra vinklar t.ex. 35° osv.) Den kurvan y=sin x som vi kommer att utgå ifrån då vi ritar kurvor av typen y=Asin(x+v).
Notera att A och v är konstanter medan x som vanligt är en variabel. Om vi får i uppgift att rita kurvan y=2sin x hur gör vi då?
Observera att tvåan motsvarar A:et i funktionen. Vi börjar med att rita upp en värdetabell för att göra det hela lite klarare och sedan för vi in värdena i grafen. y-värdena är, i detta fall, värdena på 2sin x.

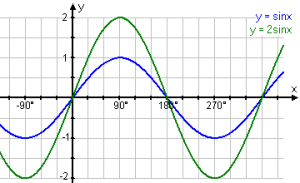
Nu när vi tittar på värdetabellen och grafen så ser vi att de har samma period, alltså i det här fallet har de båda 360° mellan varje topp alternativt mellan varje dal. Det som skiljer kurvorna åt är att y=2sin x har dubbelt så stora y-värden som y=sin x har. Det betyder att man kan rita kurvan y=2sin x genom att fördubbla värdena på sin x. Det är ju hur logiskt som helst vi tar alltså sin x multiplicerat med 2 precis som det står i den funktionen.
Samma sak som vi har gått igenom med sinuskurvan händer också med cosinuskurvan, den enda skillnaden är att cosinuskurvan har andra värden.
Viktigt!
Konstanten A har alltså den funktionen att den drar ut kurvan på höjden.
Vi kallar talet A för amplituden.
Om A är en positiv konstant så är största värdet A och minsta värdet -A för kurvan y=Asin x.
Värdemängden till funktionen är
Amplituden är avståndet från mitten på kurvan (om man skulle dra en vågrät linje genom mitten på den) och upp/ner till den punkt där kurvan vänder, alltså största eller minsta värdet hos kurvan. För att räkna ut amplituden på ett lätt sätt så tar du det största värdet minus det minsta värdet och delar det sedan med 2.
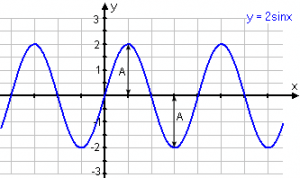
Då går vi in lite mer på begreppet sin(x+v). Om vi lägger till eller tar bort ett visst gradantal så kommer sinus- eller cosinuskurvan att flytta sig i sidled. Ta t.ex. sin(x+30°) som visar oss att kurvan kommer flytta sig 30°, men åt vilket håll? Det första man tänker på är att då man plussar på 30° så blir ju vinkeln större och man flyttar kurvan åt höger, och då man tar minus 30° blir vinkeln mindre och därmed flyttas kurvan åt vänster. MEN, ack så fel det är. Tyvärr så är det precis tvärtom; lägger du till grader förskjuts kurvan åt vänster och drar du ifrån så förskjuts den åt höger. Dumt va? Men låt mig förklara varför:
Då vi skriver y=sin(x+30°) så är det viktigt att veta att vi alltid utgår från vinklarna 0°, 90°, 180°, 270° och 360°. Det innebär att talen x och 30° tillsammans bildar dessa vinklar. För att vi ska kunna rita upp kurvan så måste vi ju ha ett värde på x, så då får vi ta och räkna ut det. Ta 90° t.ex: x+30°=90° –> x=90°-30°=60°.
Till skillnad från y=sin x-kurvans 90° så hamnar y=sin(x+30°) istället på 60° och det är därför man förskjuter kurvan åt vänster då man adderar en vinkel.
Hade det stått y=sin(x-30°) så skulle vi räkna ut x på följande vis:
x-30°=90° –> x=90°+30°=120°
Se där, 120°, vi flyttar alltså kurvan åt höger.
Viktigt!
Om v är en positiv vinkel så innebär en förskjutning på v grader åt höger av kurvan y=sin x.
Om v är en positiv vinkel så innebär en förskjutning på v grader åt vänster av kurvan y=sin x.
Detta gäller även för kurvan cos x!
Rita kurvan och ange kurvans läge i förhållande till till
Lösning
Rita först upp en värdetabell:

Sedan ritar vi upp den genom att värdena på sin(x+60) är våra y-värden och x-värdena har vi ju också räknat ut. För att vara lite övertydlig kan vi även rita in kurvan y=sin x för att tydligt se skillnaden mellan de båda. Vi skulle även ange kurvans läge i förhållande till y=sin x och därför svarar vi att kurvan sin(x+60°) är förskjuten 60° åt vänster i förhållande till y=sin x.
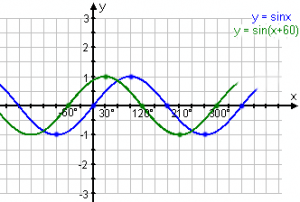
Hoppas att ni inte tyckte det var alltför krångligt. Vi tar ett exempel till där vi även måste ta hänsyn till amplituden.
Rita kurvan och ange kurvans läge i förhållande till till
Lösning
Okej, vi börjar i vanlig ordning med att rita upp en värdetabell. Den här gången är det dock viktigt att vi skriver in värdet för -2,5cos x och inte bara cos x, t.ex. cos 0°=1 och sen multiplicera det med (-2,5) –> -2,5.

Sådär, nu är det bara för oss att återigen fylla i de punkter vi har fått fram och sedan rita en fin cosinuskurva. Om du vill kan du även rita upp y=cos x ifall det underlättar för dig att svara på i vilket läge vår kurva är i förhållande till y=cos x. Däremot känner du att du har koll på läget och vet att kurvan förflyttas, i detta fall, 30° åt höger så är ju det jätte bra. Kom ihåg, är det minus flyttas kurvan åt höger, och är det plus flyttas den åt vänster så många grader som är angett.

Vi skulle även ange värdemängden för kurvan. Värdemängden är det intervall på y-skalan som y kan anta. Eftersom vi kan se i både värdetabellen och i grafen at det minsta respektive största värdet som funktionen når på y-axeln är -2,5 respektive 2,5 så blir alltså värdemängden:
Svar
Kurvan är förskjuten 30° åt höger och dess värdemängd är
Vi går även in på ett tredje exempel för att lära oss ytterligare en sak.
Kurvorna i uppgift a) och b) kan skrivas på formen Ange kurvornas ekvationer på denna form.
Lösning till a)

Talet A kallades ju för amplituden. Här ser vi att kurvan går från mitten och upp till 1,5 på y-axeln innan den vänder, därför blir A=1,5.
Då jag ska beräkna förskjutningen i sidled brukar jag alltid titta på den delen av sinuskurvan som bryter y-axeln. I kurvan y=sin x bryter den y-axeln i origo, en ganska lättöverskådlig punkt att utgå ifrån. Längre fram i detta avsnitt är det dock inte säkert att man kan utgå från origo, men mer om detta senare. I bilden här ovan så ser vi att kurvan är förskjuten 60° åt höger vilket innebär att det måste stå (x-60°).
Svar
Ekvationen för kurvan ser alltså ut så här: y=1,5sin(x-60°)
Lösning till b)
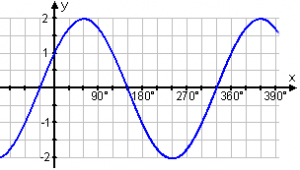
Amplituden för denna kurva är 2 och kollar vi i origo, där y=sin x normalt passerar genom så ser vi att linjen är förskjuten 30° åt vänster, vilket ger oss (x+30°).
Svar
Kurvans ekvation är y=2sin(x+30°)
17 januari 2011 @ 18:59
Om v är en positiv vinkel så innebär y= \\sin(x-v) en förskjutning på v grader åt höger av kurvan y=sin x.
Om v är en positiv vinkel så innebär y= \\sin(x v) en förskjutning på v grader åt vänster av kurvan y=sin x.
Detta gäller även för kurvan cos x!
ska det stå om v är en positiv vinkel på både y= \\sin(x-v) och y= \\sin(x+v) ?
17 maj 2011 @ 13:24
I början av exempel 4 skriver du att kurvan y=-2,5cos(x-60) ska ritas. Bör det inte istället stå y=-2,5cos(x-30) där, eftersom att 30 är gradtalet du använder dig av i lösningen av uppgiften?
23 maj 2012 @ 21:43
Kung lärare, tack,
20 maj 2013 @ 5:31
Exempel 3 är fel, det står 60 grader i frågeställningen och 30 grader i lösningen