Matte E - Differentialekvationer
Ekvationer av första ordningen
Bland ekvationer av första ordningen finns det två sorters differentialekvationer, nämligen homogena och inhomogena.
Homogena
Det karakteristiska utseendet för en homogen differentialekvation är
där a är en konstant.
Dessa ekvationer har lösningarna:
där C är en konstant.
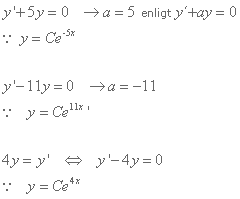
Var uppmärksam på om y’ har en konstant framför sig, du kan nämligen inte använda formeln och få ett korrekt svar om du inte har sambandet y’ + ay = 0.

Inhomogena
Det karakteristiska utseendet för en inhomogen differentialekvation är:
där g(x) är antingen en konstant eller ett polynom och beroende på det så har de olika lösningar.
Ekvationen har lösningarna
För ekvationen
gäller följande:
“Om i och är ett polynom så finns en speciell lösning, alltså som är ett polynom av samma grad som g.”
För att räkna ut den så kallade allmänna lösningen av inhomogena ekvationer så adderar man den speciella lösningen till den ekvation man skulle få fram om ekvationen y’+ay = g(x) vore homogen.
Bestäm samtliga lösningar till differentialekvationen:
a.)
b.)
a.) Den speciella lösningen är:
Den andra lösningen är:
Den allmänna lösningen blir därför:
b.) Den speciella lösningen är:
Den andra lösningen är: Dividera bort trean från y’.
Den allmänna lösningen:
a) För att få ut den speciella lösningen så måste vi ta 8 delat med 2 enligt ys=k/a. Tänk såhär: Den speciella lösningen heter ju y och inget annat. Står det då 2y i ekvationen måste vi ju först dela med 2 för att få fram enbart y, eller hur? Därmed delas även (8:an, k=8) med 2. Sedan ska vi ha den andra lösningen som räknas ut som om 8:an hade varit en nolla, enligt regeln för de homogena ekvationerna. Den allmänna lösningen blir således den speciella lösningen plus den andra lösningen.
b) Vi börjar även här med att lösa ut den speciella lösningen vilket blir 6/9 som förkortas till 2/3. Sedan ska vi ha den andra lösningen som räknas ut som om 6 hade varit 0, enligt regeln för de homogena ekvationerna. Den regeln gäller för då det står en 1:a framför y’, vilket det inte gör i detta fall och vi måste då dela med 3 för att få bort 3:an framför y’.
Den allmänna lösningen fås genom att lägga ihop den speciella lösningen med den andra lösningen.
Då g(x) är ett polynom så använder vi oss av ett litet annorlunda sätt:
Lös differentialekvationen
Då x2 finns så finns även ett tal med x1 och x0.
Sätt in de båda lösningarna i uttrycket:
Detta ovan gäller för alla x och det ger oss ekvationssystemet:
Vilket ger lösningen (A, B, C) = (1, -2, 2).
Alltså är en lösning.
Svar:
30 april 2010 @ 9:36
Ska det inte stå:
yS’ = 2Ax+B
på exempel 4?
31 maj 2010 @ 22:18
Jo, jag tycker också att det borde stå 2Ax + B
1 juni 2010 @ 16:46
Det var en typo, som ni också såg så var svaret rätt även fast det var felskrivet halvvägs i lösningen
18 februari 2011 @ 18:08
Hej. Jag minns att vi räknade med Integrerande Faktorer när vi räknade med linjära differentialekvationer av första graden i gymnasiet. Både homogena och inhomogena. Var det bara våran klass som fick lära oss det eller?
14 december 2012 @ 16:25
nbm
25 januari 2016 @ 14:51
wow