Matte E - Differentialekvationer

Beräkna med Eulers metod ett närmevärde med tre gällande siffror till y(2) för lösningen till Välj steglängden 0,5.

Okej, vi har alltså fått följande info:
- Vi kan plocka ut uttrycket y+2 och sätta in i vår parentes för funktionen.
- Våra startkoordinater alltså (x₀, y₀) är (0, 3).
- Vi vet att vi ska fortsätta räkna fram tills dess att vi har nått x-värdet 2.
- Vi ska använda oss av steglängden 0,5, alltså h=0,5.
Innan vi sätter igång och räknar vill jag bara påpeka en sak. För att göra det enkelt för oss kan vi på förhand räkna ut hur många steg det tar med steglängden h=0,5  innan vi har kommit fram till x=2.

steg.

Jag kollar avståndet mellan startpunkten och målet vilket blir 2. Det avståndet delar vi med antalet steg och det kommer alltså att ta 4 steg innan vi är framme. Då är det bara att börja räkna!

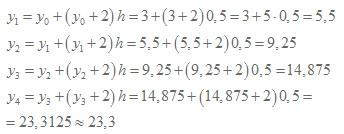
Vi börjar med y₁, vi sätter in värdet på y₀ som är 3 och värdet på h som är 0,5 och får då fram y-värdet 5,5. Då vi sedan ska beräkna y₂ så använder vi oss av det föregående värdet på y alltså y₁. y₁ kom vi ju nyss fram till det var lika med 5,5. (Notera att hade x varit med i detta tal hade vi behövt göra en liknande uträkning på det också. Se längre fram i nästa exempel för att även räkna med x).
I alla fall, vi tar alltså värdet från y₁ och stoppar in det i formeln som räknar ut y₂. När vi sedan räknar ut y₃ så använder vi oss av det värde vi fick fram på y₂ osv. Steglängden h är alltid densamma.
När vi nått y₄ så vet vi att det är y₄:ans värde vi är ute efter eftersom vi räknade ut att det skulle krävas 4 steg innan vi kom fram till x=2 och därmed är svaret lite avrundat 23,3.

Beräkna med Eulers metod ett närmevärde med tre gällande siffror till y(1) för lösningen till Välj steglängden 0,2.

Okej, snabb överblick ger oss att våra startkoordinater är (0, 2), det vi ska sätta in i parentesen är xy+1, steglängden h är 0,2 och vi ska ta reda på y-värdet i den punkt där x=1.
Vi gör den lilla snabba uträkningen på hur många steg som krävs innan vi är framme vid x=1.

steg.

Sådär, då kan vi börja.

Då det kommer att bli en förbaskat massa decimaler nu när vi fortsätter så kommer jag att beräkna resten genom att spara talen i miniräknaren. Därmed kan jag fortsätta räkna med det exakta antalet decimaler fast jag skriver dem som avrundade tal på pappret.

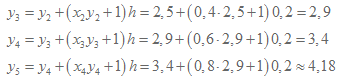
Japp, svaret blir, avrundat förstås, 4,18. Precis som innan så använder vi startvärden (x₀, y₀) för att räkna ut y₂ och kommer då fram till y₂=2,2. När vi ska räkna ut y₂ så använder vi oss av y₁-värdet. Notera här att vi även har med ett x i detta tal, och hur får vi fram x₁? Jo, steglängden vi har går ju i linje med x-axeln eftersom vi förflyttar oss längs den, från x=0 till x=1, eller hur. För varje y vi räknar ut har vi tagit ett steg där steglängden är 0,2, alltså lägger vi till 0,2 på x-värdet för varje steg. x₁ är därmed x₀+0,2=0,2, piece of cake!
Sedan fortsätter det så här fram tills det 5:e steget som vi tidigare räknade ut var det sista.

När det gäller x-punkterna så låt dig inte luras av att x=0,8 i femte steget. Det x-värdet du ser där är ju värdet på x₄ alltså får vi i vårt huvud räkna ut att när vi är inne på femte steget så är x₅=0,8+0,2=1 och då är vi framme. Detta visar att då vi har med x i uträkningarna så måste vi egentligen inte räkna ut hur många steg det blir i förväg, eftersom man lika gärna kan hålla koll på det under tidens gång. För min del så föredrar jag att räkna ut den i förväg så vet jag med säkerhet när jag ska stanna.