Matte F - Integraler
Partiell Integrering
Inledning med exempel
Fram tills nu så har vi löst integraler med en produkt i sig med hjälp av substitution eller med trigonometriska omskrivningar (för att till exempel lösa ). Fram tills nu!
Partiell integrering kan man tänka sig att det är Produkt-Integrering, precis som i derivering. Det här är emellertid mycket svårare och går ut på att man integrerar den ena faktorn och deriverar den andra. Här går vi dock igenom den icke-officiella metoden. Metoden vi inte går igenom här är mycket mer komplex, och är den man går igenom på universitetet. Metoden vi visar här är i grunden samma sak, fast det är en förenkling. Man får samma svar, fast det är mycket enklare att utföra och hålla reda på termerna.
Först visar vi hur man gör, sedan följer förklaringen.
Integrera .
Så här skriver man för hand när man räknar:
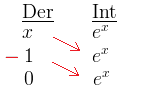
Svar: .
Metoden är som min lärare beskrev “mördande effektiv”. Precis som nämndes innan exemplet så deriveras ena faktorn, och den andra integreras. Man ska välja att derivera den termen som kommer bli noll efter några deriveringar.
Om ingen av faktorerna kommer att blir noll efter några deriveringar så får man derivera och integrera några gånger för att sedan “bryta”. Hur man bryter och vad man gör efter det visar vi längre ner.
Vidare i denna metod ska man sätta ett minus framför varannat tal i vänstra kolumnen (röd färg). Man sätter alltid minuset först framför den andra termen. Viktigt att komma ihåg är att man sätter ut dessa minus efter att man har deriverat och integrerat klart. Det framgår och blir mer självklart efter några exempel till. Pilarna som man ritar ut är hur man multiplicerar (röda), och de ritas alltid ut på samma sätt som visas här. Blir det fler deriveringar innan det blir noll så blir det fler pilar och fler minus, såklart. x multipliceras alltså här med ex, -1 multipliceras med ex. Dessa multiplikationer adderas ihop, det är därför det blir minus ex i svaret. Enkelt!
Mer exempel!
Integrera .
Då ska det vara tydligt att vi väljer att derivera x2 eftersom den faktorn kommer att bli noll efter några deriveringar.

Kom ihåg att skriva ut vartannat minus och pilarna. Pilarna för att vara tydlig med vilken term som man ska multiplicera med vilken. Sedan är det bara att pussla ihop talen!
Som då också är vårt svar ![]()
Exempel med intervall
Vi kan ta ett till exempel innan vi visar ett där man måste bryta. Vi kan ta ett exempel med intervall:
Lös .
Inga förklaringar för nu borde det vara tydligt vad som händer ![]()
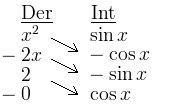
Så vi får:
Svar: .
Det kan verka förvirrande att inte ha någon “inre derivata” eller “inre integral” eller behöva dela med 3 och x3 med bråkstreck och allt sådant. Men detta är en lösningsmetod så man kan slippa tänka på dem. Partiell integrering är en extremt kraftfull lösningsmetod och måste ofta användas eftersom det blir på tok för invecklat med inre derivator och integraler osv.
Exempel med brytning
Produkten ser inte alltid ut så som de gjort i de tidigare exemplen. Ibland kanske integralen är sin x gånger cos x, och då finns det ju ingen av faktorerna som man kan derivera ner till noll. Då finns det en speciell snits man använder. Kolla!
Lös .
Här till exempel kan man ju inte derivera någon av talen så det blir noll. Då får man derivera och integrera några gånger, följt av en brytning. Integreringen brukar vara svårare än deriveringen så man brukar välja att integrera den “enkla” och ha den i den högra spalten. Man kan självklart välja vilken man vill, och få samma svar – men det brukar underlätta att sätta den enklaste faktorn att integrera.
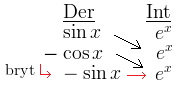
Det som är rött här visar vad som är nytt. Märk att minuset ska läggas till efter att tabellen är ifylld. Bryter man så får man en extra pil som går direkt till höger, och som vanligt visar de pilarna hur man ska multiplicera. Den nya krokiga pilen är bara en “flagga” för att visa var man bryter. Man kan derivera/integrera så många steg man vill men helst ska man bryta där man fått något som i horisontellt led ser likadant ut som faktorerna i start-integralen.
Efter brytningen får vi alltså:
Alltså brytningen ger oss en “rest-integral”. Det som är kvar av integralen när man bantat den lite.
Observera nästa steg:
Man får se på talet med ett annat öga! Hela högra ledet av talet var ju lika med vänster led. Vi kan alltså ta i båda led. Coolt va?
Dela på 2 i båda led:
Och där har ni svaret! Man kommer fram till svaret på integralen från ett helt annat håll ![]()
Helt klart ur-ballt.
Vem har inte någon gång funderat på vad integralen av ln x är? Alltså, alla “vet” ju att derivatan av ln x är 1/x, men vad är egentligen integralen? (Hur man deriverar den visade vi ju i avsnittet om implicit derivering.) Vi löser det vettja!
Lös integralen .
För att lösa denna integral behöver vi göra partiell integrering, men vi har ju problemet med att vi endast har en faktor. Då får vi helt enkelt lägga till en faktor och sedan göra partiell integrering:
Och härifrån gör vi vår vackra tabell:
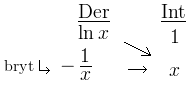
Vi deriverar ln x och integrerar 1, för annars kommer vi ju ingenstans. Vi bryter nästan direkt för då kommer vår “rest-integral” bli enkel.
Och där är vi klara! Enkelt!
Svar: .
Lös integralen .
a.) Med substitutionsmetoden.
b.) Med partiell integrering.
a.)
b.)
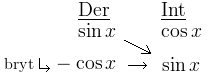
Vidare:
Båda metoderna fungerar fint. Det handlar mest om vilken man föredrar ![]()
29 november 2012 @ 14:25
Finns det en allmän formel för hur man räknar ut integralen av f(f(x)), dvs i explicit form? Eller en omvänd kjedjeregel om man kan kalla det så!